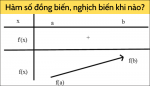
Nội dung bài học này làm sao biết được khái niệm thế nào là hàm số đồng biến, hàm số nghịch biến điều kiện để hàm số đơn điệu trên một miền. Ở các lớp trước chúng ta đã hiểu hàm số y = f(x) là đồng biến nếu giá trị của x tăng, nghịch biến nếu giá trị của x tăng nhưng giá trị của f(x) giảm. Vậy quy tắc xét tính đơn điệu ( hàm số luôn đồng biến hoặc nghịch biến trên khoảng xác định K ) như thế nào? chúng ta cùng nhau đi tìm hiểu và lấy ví dụ minh họa.
Định nghĩa
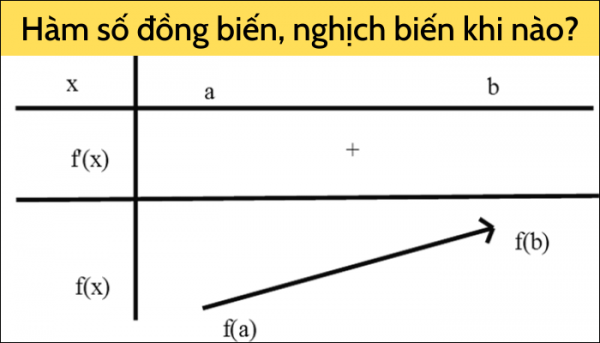
Hàm số y = f(x) đồng biến (tăng) trên K ⇔ ∀x1, x2 ∈ K, x1 < x2 thì f(x1) < f(x2).
Hàm số y = f(x) nghịch biến (giảm) trên K ⇔ ∀x1, x2 ∈ K, x1 < x2 thì f(x1) > f(x2).
Kí hiệu K là một khoảng, một đoạn hoặc một nửa khoảng.
Điều kiện cần để hàm số đơn điệu:
Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
– Nếu hàm số đồng biến trên khoảng K thì f'(x) ≥ 0, ∀ x ∈ K .
– Nếu hàm số nghịch biến trên khoảng K thì f'(x) ≤ 0, ∀ x ∈ K.
Điều kiện đủ để hàm số đơn điệu:
Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
– Nếu f'(x) > 0, ∀x ∈ K thì hàm số đồng biến trên khoảng K.
- Trọng tâm tam giác vuông, cân: Tính chất, Công thức và Cách tính tọa độ.
- Bảng đơn vị đo diện tích – Đổi đơn vị đo diện tích mét vuông lớp 4.
– Nếu f'(x) < 0, ∀x ∈ K thì hàm số nghịch biến trên khoảng K.
– Nếu f'(x) = 0, ∀x ∈ K thì hàm số không đổi trên khoảng K.
* Chú ý.
– Nếu K là một đoạn hoặc nửa khoảng thì phải bổ sung giả thiết “ Hàm số y = f(x) liên tục trên đoạn hoặc nửa khoảng đó”. Chẳng hạn: Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và có đạo hàm f'(x) > 0, ∀x ∈ K trên khoảng (a; b) thì hàm số đồng biến trên đoạn [a; b].
– Nếu f'(x) ≥ 0, ∀x ∈ K ( hoặc f'(x) ≤ 0, ∀x ∈ K ) và f'(x) = 0 chỉ tại một số điểm hữu hạn của K thì hàm số đồng biến trên khoảng K ( hoặc nghịch biến trên khoảng K).
Quy tắc xét tính đơn điệu của hàm số
- Tìm tập xác định
- Tính đạo hàm f'(x). Tìm các điểm xi (i= 1 , 2 ,…, n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
- Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Phương pháp giải bài tập :
1. Lập bảng xét dấu của một biểu thức P(x)
Bước 1. Tìm nghiệm của biểu thức P(x), hoặc giá trị của x làm biểu thức P(x) không xác định.
Bước 2. Sắp xếp các giá trị của x tìm được theo thứ tự từ nhỏ đến lớn.
- Số chẵn số lẻ là gì? Số chẵn là những số nào, số lẻ là những số nào?
- Số lớn nhất có 1,2,3,4,5 chữ số chẵn lẻ khác nhau là chữ số nào?
Bước 3. Sử dụng máy tính tìm dấu của P(x) trên từng khoảng của bảng xét dấu.
2. Xét tính đơn điệu của hàm số y = f(x) trên tập xác định
Bước 1. Tìm tập xác định D.
Bước 2. Tính đạo hàm y’ = f'(x).
Bước 3. Tìm nghiệm của f'(x) hoặc những giá trị x làm cho f'(x) không xác định.
Bước 4. Lập bảng biến thiên.
Bước 5. Kết luận.
3. Tìm điều kiện của tham số m để hàm số y = f(x) đồng biến, nghịch biến trên khoảng (a; b) cho trước.
Cho hàm số y = f(x, m) có tập xác định D, khoảng (a; b) ⊂ D:
– Hàm số nghịch biến trên (a; b) ⇔ y’ ≤ 0, ∀ x ∈ (a; b)
– Hàm số đồng biến trên (a; b) ⇔ y’ ≥ 0, ∀ x ∈ (a; b)
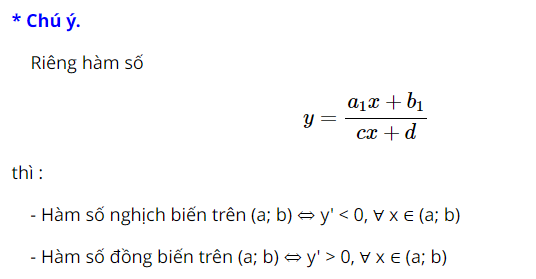
Xem thêm tại đây :
Tính chất và dấu hiệu nhận biết hình thang cân, vuông.