Hình thang là gì? Dấu hiệu nhận biết hình thang và các tính chất hình thang cân, vuông mà các bạn cần lắm rõ lý thuyết về hình thang.
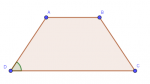
Hình thang là gì ?
Hình thang là tứ giác có hai cạnh đối song song.
Hai cạnh song song gọi là hai đáy.
Hai cạnh còn lại gọi là hai cạnh bên.
Dấu hiệu nhận biết hình thang.
Nhận biết về hình thang chúng ta có 5 dấu hiệu nhận biết đó là
Tứ giác có hai cạnh đối song song.
Hình thang có một góc vuông là hình thang vuông
Hình thang có hai góc kề một đáy là hình thang cân
Hình thang có hai cạnh bên bằng nhau là hình thang cân
Hình thang có hai đường chéo bằng nhau là hình thang cân
công thức tính diện tích hình thang
Tính chất của hình thang
tính chất về góc
- Hai góc kề một cạnh bên của hình thang có tổng bằng 180 độ (nằm ở vị trí trong cùng phía của hai đoạn thẳng song song là 2 cạnh đáy).
- Đối với hình thang cân thì hai góc kề một cạnh đáy bằng nhau.
Tính chất về cạnh
- Hình thang có 2 cạnh đáy bằng nhau thì hai cạnh bên sẽ song song và bằng nhau.
- Ngược lại, nếu hình thang có 2 cạnh bên song song thì chúng sẽ bằng nhau và 2 cạnh đáy bằng nhau.
- Hình thang cân có 2 đường chéo bằng nhau.
Tính chất về đường trung bình
- Đường trung bình là đường thẳng nối trung điểm hai cạnh bên của hình thang.
- Tính chất 1: Đường thẳng đi qua trung điểm 1 cạnh bên của hình thang và song song với 2 cạnh đáy thì sẽ đi qua trung điểm của cạnh bên còn lại.
- Tính chất 2: Đường trung bình của hình thang sẽ song song với 2 cạnh đáy và bằng ½ tổng 2 đáy.
Có mấy 3 hình thang
Hình thang vuông
Hình thang cân
Hình thang vuông cân còn được gọi là hình chữ nhật
Như vậy ta có nhận xét như sau :
Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
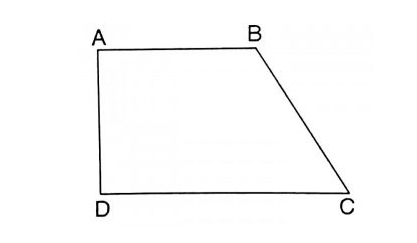
Tính chất hình thang vuông
Định nghĩa hình thang vuông:
Hình thang vuông là hình thang có một góc vuông. Hình thang vuông là 1 trường hợp đặc biệt của hình thang .
Dấu hiệu nhận biết bình thang vuông
Dấu hiệu nhận biết: Hình thang có một góc vuông là hình thang vuông.
Hình thang vuông là một trường hợp đặc biệt của hình thang.
Ví dụ chứng minh hình thang vuông
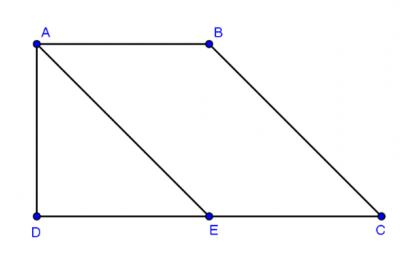
Cho hình thang ABCD, đáy AB = 40 cm , CD = 80 cm, cạnh bên BC = 50 cm và AD = 30 cm. Yêu cầu: Chứng minh ABCD là hình thang vuông.
Lời giải
Từ đỉnh A kẻ đường thẳng song song với BC và cắt DC tại E.
Ta có: AE = BC = 50 cm; EC = AB = 40 cm
=> DE = 80 – 40 = 40 cm
Tam giác ADE có AD = 30 cm, DE = 40 cm và AE = 50 cm
nê AD² = 30² = 900 cm , DE² = 40² = 1600 cm , AE² = 50² = 2500
AE² = AD² + DE² theo định lý pitago đảo cho tam giác vuông ADE
suy ra  = D =90° suy ra tứ giác ABCD là hình thang vuông
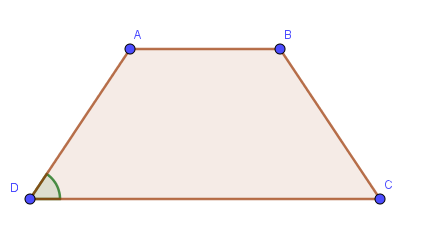
Tính chất hình thang cân
Định nghĩa hình thang cân :
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Tính chất hình thang cân
Hai cạnh bên bằng nhau.
Hai góc kề cạnh đáy bằng nhau.
Hai đường chéo bằng nhau.
Hình thang cân nội tiếp đường tròn
Chứng minh như sau :
Định lí 1: Trong một hình thang cân, hai cạnh bên bằng nhau, ABCD là hình thang cân (đáy AB, CD) => AD = BC
Định lí 2: Trong một hình thang cân, hai đường chéo bằng nhau, ABCD là hình thang cân (đáy AB, CD) => AC =
BD
Định lí 3: Hình thang có hai đường chéo bằng nhau là hình thang cân. Hình thang ABCD (đáy AB, CD) có AC = BD
=> ABCD là hình thang cân.
Dấu hiệu nhận biết hình thang cân
Dấu hiệu nhận biết hình trang cân
Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân. Hình thang có hai đường chéo bằng nhau là hình thang cân.
Hình thang có hai trục đối xứng của hai đáy trùng nhau là hình thang cân
Hình thang có hai cạnh bên bằng nhau (nếu hai cạnh bên ấy không song song) là hình thang cân.
Hình thang nội tiếp đường tròn là hình thang cân .