Phương trình mũ, phương trình lôgarit và phương trình lũy thừa là những dạng bài tập luôn nằm trong các đề thi THPT cuối cấp, Vậy Phương trình logarit là gì? có những dạng nào và dùng phương pháp gì để giải? Bài viết dưới đây chúng tôi sẽ tổng hợp tất cả các kiến thức có liên quan đến phương trình logarit. Hi vọng giúp các em có kiến thức để vận dụng giải bài tập.
PHƯƠNG TRÌNH LOGARIT CƠ BẢN
Với cơ số a dương và khác 1 thì phương trình có dạng như sau được gọi là phương trình lôgarit cơ bản
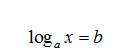
Ta thấy vế trái của phương trình là hàm đơn điệu có miền giá trị là R. Vế phải phương trình là một hàm hằng. Vì vậy phương trình lôgarit cơ bản luôn có nghiệm duy nhất. Theo định nghĩa của logarit ta dễ dàng suy ra nghiệm đó là
x = a^b
CÁCH GIẢI PHƯƠNG TRÌNH LOGARIT
Các phương trình lôgarit nói chung đều cần phải đưa về phương trình dạng đơn giản hơn để giải. Để đưa về phương trình dạng đơn giản người ta thường dùng 1 số phương pháp như: Đưa về cùng cơ số; Đặt ẩn phụ; Mũ hóa. Ngoài ra còn một số phương pháp cũng có thể sử dụng như: Dùng đồ thị hàm số; Dùng tính đơn điệu của hàm số để đánh giá. Sau đây chúng ta sẽ đi phân tích từng phương pháp thông qua các ví dụ nhé.
Xem thêm tại đây :
- Phương trình mũ là gì? Bất phương trình và các phương pháp giải phương trình mũ
- Tìm tập giá trị của hàm số logarit và Bài tập vận dụng
- Hàm số lôgarít là gì? Khảo sát và phân dạng hàm số lôgarít
1. GIẢI PHƯƠNG TRÌNH LOGARIT BẰNG CÁCH ĐƯA VỀ CÙNG CƠ SỐ
Một lưu ý nhỏ là trong quá trình biến đổi phương trình lôgarit, chúng ta thường quên việc kiểm soát miền xác định của phương trình. Vì vậy để cho an toàn thì ngoài phương trình lôgarit cơ bản, các bạn nên đặt điều kiện xác định cho phương trình trước khi biến đổi.
Ví dụ :
Giải phương trình sau :
![]()
Bài làm :
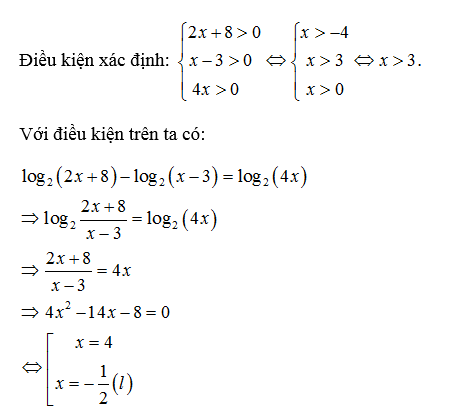
Vậy phương trình đã cho có nghiệm x = 4.
2. GIẢI PHƯƠΝG TRÌNH LOGARIT BẰNG CÁCH ĐẶT ẨN PHỤ
phương pháp :
![]()
Ta chú ý công thức đổi cơ số:
![]()
Ví dụ : Giải phương trình :
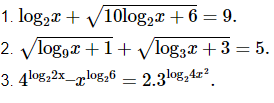
Bài làm :
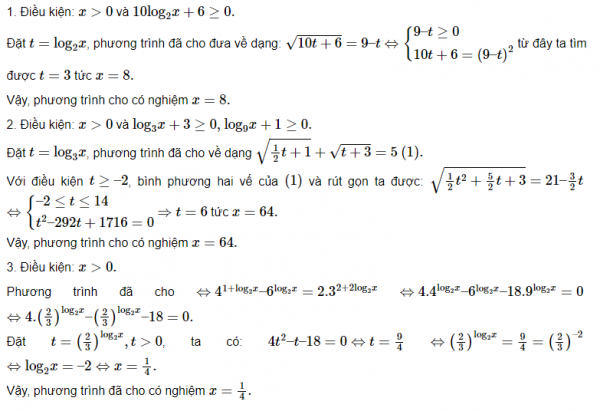
Dạng 3. Biến đổi phương trình về dạng tích
phương pháp ![]()
Ví dụ :

Nội dung tìm hiểu thêm :
- Quy tắc tính, Cách học thuộc công thức Lôgarit nhanh nhất
- Bảng tóm tắt công thức Lôgarit và bài tập vận dụng
- Chuyên đề : Toán lũy thừa lớp 7 nâng cao
4. Phương pháp đồ thị
Phương pháp:
Giải phương trình: ![]()
là phương trình hoành độ giao điểm của 2 đồ thị ![]()
Khi đó ta thực hiện 2 bước:
+ Bước 1: Vẽ đồ thị các hàm số: ![]()
+ Bước 2: Kết luận nghiệm của phương trình đã cho là số giao điểm của đồ thị.
Ví dụ : Giải phương trình ![]()
Bài làm :
Điều kiện x > 0

5. Giải bất phương trình logarit
Ví dụ Giải bất phương trình:


