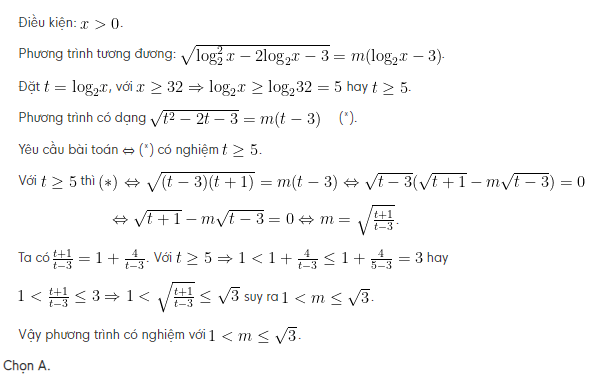Phương trình là các dạng toán vô cùng phổ biến trong toán học 12 bao gồm có trong các bài tập và đề thi, Phương trình mũ, phương trình lôgarit và phương trình chứa tham số có định nghĩa, phương pháp giải như thế nào thì trong bài này chúng ta cùng nhau đi tìm hiểu sâu về Phương trình mũ là gì? Bất phương trình và các phương pháp giải phương trình mũ, Mời các bạn cùng tìm hiểu.
Phương trình mũ cơ bản là gì ?
Phương trình ax=m(0<a≠1) được gọi là phương trình mũ.
– Với m>0 thì phương trình có nghiệm duy nhất x=logam.
– Với m≤0 thì phương trình vô nghiệm.
Xem thêm tại đây :
- Tìm tập giá trị của hàm số logarit và Bài tập vận dụng
- Hàm số lôgarít là gì? Khảo sát và phân dạng hàm số lôgarít
- Khái niệm hàm số mũ là gì? Tính chất và Đạo hàm của hàm số mũ
Bất phương trình mũ :
+ Bất phương trình mũ cơ bản
Xét phương trình a^x > b
Nếu b < hoặc = 0, tập nghiệm của bất phương trình là R vì a^x > 0 với mọi x thuộc R
Nếu b > 0 thì bất phương trình tương đương với a^x > a logab
Nếu a > 1 thì nghiệm của BPT là x > logab
Nếu 0< a < 1 thì thì nghiệm của BPT là x < logab
+ Giải bất phương trình bằng phương pháp đưa về cùng một cơ số.
+ Giải bất phương trình mũ bằng phương pháp đặt ẩn dụ.
Một số phương pháp giải phương trình mũ
Dạng 1: Phương pháp đưa về cùng cơ số.
Phương pháp:
– Bước 1: Biến đổi các lũy thừa về cùng cơ số.
– Bước 2: Sử dụng kết quả ![]()
– Bước 3: Giải phương trình f(x)=g(x) ở trên và kết luận.
Dạng 2: Phương pháp đặt ẩn phụ.
Phương pháp:
– Bước 1: Tìm một lũy thừa chung, đặt làm ẩn phụ và tìm điều kiện cho ẩn.
– Bước 2: Giải phương trình chứa ẩn phụ, kiểm tra điều kiện.
– Bước 3: Thay ẩn phụ và giải phương trình đối với ẩn ban đầu.
– Bước 4: Kết luận nghiệm.
Dạng 3: Phương pháp logarit hóa.
Phương trình có dạng
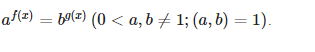
Phương pháp:
– Bước 1: Tìm điều kiện xác định.
– Bước 2: Lấy logarit cơ số a (hoặc b) hai vế: ![]()
– Bước 3: Giải phương trình trên tìm x.
– Bước 4: Kiểm tra điều kiện và kết luận.
Dạng 4: Phương trình đưa về phương trình tích.
Phương pháp:
– Bước 1: Tìm điều kiện xác định (nếu có)
– Bước 2: Biến đổi phương trình về dạng tích AB=0⇔[A=0, B=0
– Bước 3: Giải các phương trình A=0,B=0 tìm nghiệm.
– Bước 4: Kiểm tra điều kiện và kết luận nghiệm.
Dạng 5: Phương pháp sử dụng bất đẳng thức, tính đơn điệu của hàm số.
Phương pháp:
– Bước 1: Tìm điều kiện xác định.
– Bước 2: Có thể làm một trong hai cách sau:
Cách 1: Biến đổi phương trình sao cho một vế là hàm số đơn điệu, một vế là hằng số hoặc một vế là hàm đồng biến và vế còn lại là hàm số nghịch biến.
Cách 2: Biến đổi phương trình về dạng f(u)=f(v) với f là hàm số đơn điệu.
– Bước 3: Nhẩm một nghiệm của phương trình trên.
– Bước 4: Kết luận nghiệm duy nhất của phương trình.
Chú ý :
- Cách tính lũy thừa trên máy tính casio fx 500ms
- Định nghĩa Lôgarit là gì? Tính chất và Các đồng nhất thức logarit
Bài tập vận dụng :
Bài tập 1 : Giải các phương trình sau:
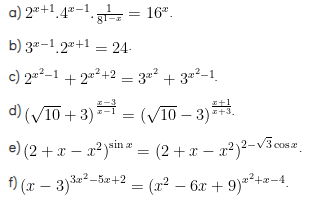
Bài giải :
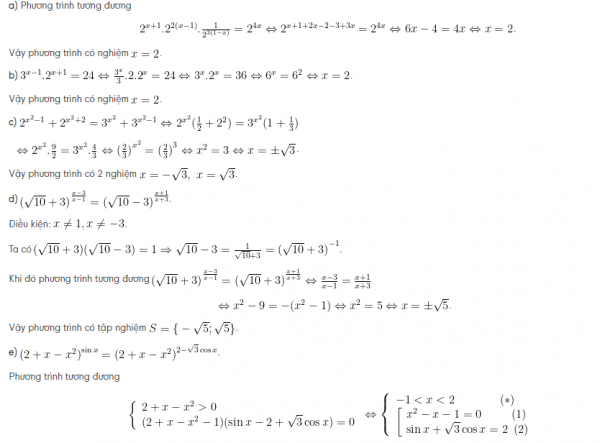

Bài 2 :
Tìm tất cả các giá trị thực của tham số m để phương trình
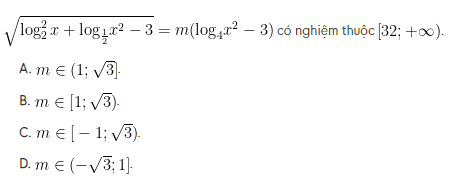
Giải bài :