Trong toán học có rất nhiều dạng bài tập khác nhau, ở bài trước chúng ta đã cùng nhau đi tìm hiểu xem thế nào là hàm số mũ, đạo hàm của hàm số mũ. Ở bài này chúng ta sẽ cùng nhau đi tìm hiểu dạng toán học về Hàm số lôgarít là gì? Khảo sát và phân dạng hàm số lôgarít, Hi vọng sẽ giúp ích được cho các em có kiến thức để giải các bài tập cũng như vận dụng vào thực tiễn.
Xem thêm tại đây :
- Khái niệm hàm số mũ là gì? Tính chất và Đạo hàm của hàm số mũ
- Quy tắc tính, Cách học thuộc công thức Lôgarit nhanh nhất
- Bảng tóm tắt công thức Lôgarit và bài tập vận dụng
Hàm số logarit:
y = logax, (a > 0, a ≠ 1)
Với a > 1
1. Tập xác định: D = (0; +∞)
2. Tập giá trị T = ℝ
3. Tính đơn điệu:
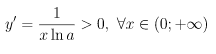
4. Giới hạn đặc biệt
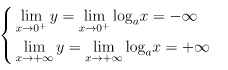
=> x = 0 là tiệm cận đứng
5. Bảng biến thiên
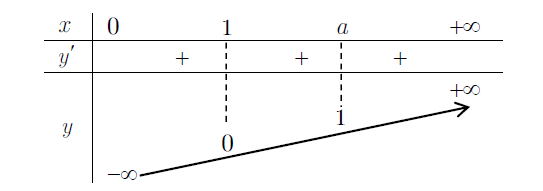
6. Đồ thị
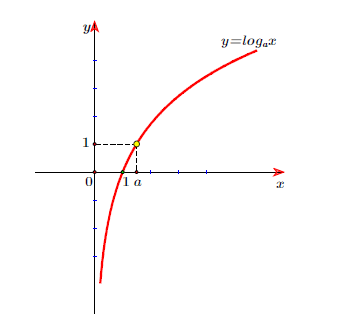
Chú ý :
Với 0 < a < 1
1. Tập xác định: D = (0; +∞)
2. Tập giá trị: T = ℝ
3. Tính đơn điệu
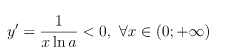
Hàm số nghịch biến trên (0; +∞)
4. Giới hiện đặc biệt
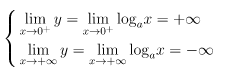
⇒ x = 0 là tiệm cận đứng
5. Bảng biến thiên
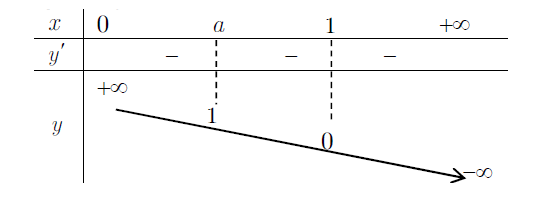
6 Đồ thị :
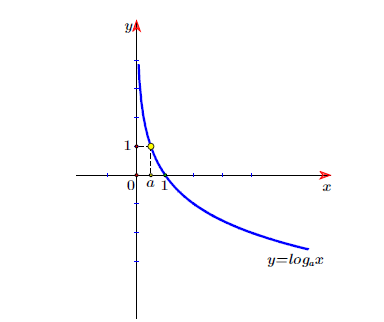
Đồ thị hàm số luôn đi qua 2 điểm A(1;0), B(a;1) và nhận trục tung làm tiệm cận đứng.
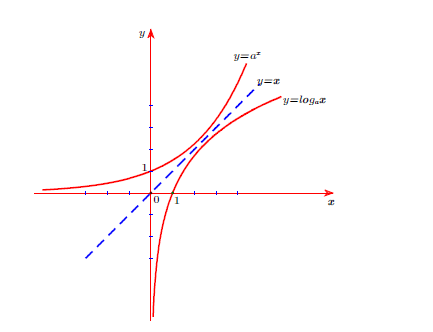
Đặc điểm chung của đồ thị hàm số y = ax và y = logax khi vẽ trên cùng hệ trục tọa độ: Hai đồ thị của hàm số luôn đối xứng nhau qua đường thẳng y = x ( Đường phân giác của góc phần tư thứ nhất và thứ ba).
Với a > 1
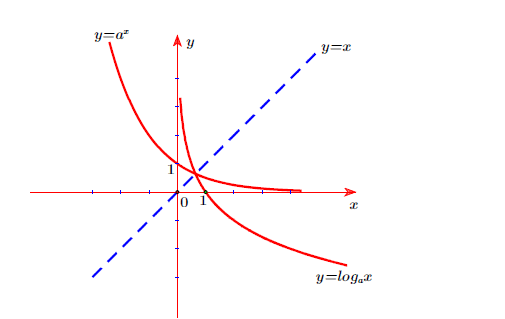
Với 0 < a <1
Phân dạng bài tập hàm số logarit
Dạng 1: Tìm tập xác định của hàm số logarit
Phương pháp
Hàm số logarit y = loga f(x) xác định 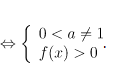
Theo tính đơn điệu của hàm số mũ và hàm số logarit ta luôn có:
Với a > 1 thì 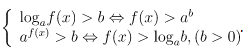
Với 0 < a < 1 thì 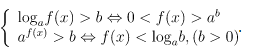
Hàm số y = loga f(x) xác định trên tập K ⇔ f(x) > 0, ∀x ∊ K.
Dạng 2: Đạo hàm và đồ thị của hàm số logarit
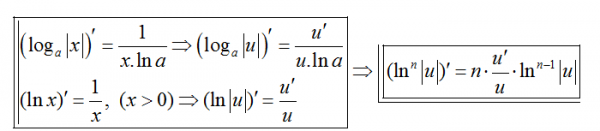
Dạng 3 : Tính chất của hàm số lôgarit y=logax (a>0,a≠1).
– Tập xác định: (0;+∞).
– Đạo hàm ∀x∈(0;+∞),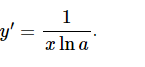
– Chiều biến thiên:
+) Nếu a>1 thì hàm số luôn đồng biến
+) Nếu 0<a<1 thì hàm số luôn nghịch biến
– Tiệm cận: Trục Oy là tiệm cận đứng
.- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).

