Để làm được các dạng bài tập có liên quan đến Lôgarit thì trước hết ta phải tìm hiểu cũng như học thật kỹ định nghĩa, công thức, Tính chất, Quy tắc của Lôgarit. Vậy làm thế nào để học được những công thức khó đó một cách nhanh nhất thì ở dưới bài này chúng tôi sẽ hướng dẫn các bạn các Quy tắc tính, Cách học thuộc công thức Lôgarit nhanh nhất. Hi vọng sẽ giúp ích được cho các bạn cũng như các em học sinh giải được bài tập một cách chính xác nhất.
Định nghĩa
Cho hai số dương a, b với a≠1.
Nghiệm duy nhất của phương trình ax=b được gọi là logab ( tức là số α có tính chất là aα=b).Như vậy logab=α⇔aα=b
Ví dụ: log416=2 vì 42=16.2.
Xem thêm tại đây :
- Bảng tóm tắt công thức Lôgarit và bài tập vận dụng
- Định nghĩa Lôgarit là gì? Tính chất và Các đồng nhất thức logarit
- Chuyên đề : Toán lũy thừa lớp 7 nâng cao
Lôgarit thập phân và lôgarit tự nhiên
Lôgarit cơ số 10 còn được gọi là lôgarit thập phân, số log10b thường được viết là logb hoặc lgb.
Lôgarit cơ số e 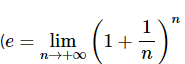
≈ 2,718281828459045) còn được gọi là lôgarit tự nhiên, số logeb thường được viết là lnb.
Quy Tắc Tính Lôgarit
Lôgarit của một tích
Định lý 1: Cho ba số dương a,b1,b2 với a≠1, ta có loga(b1b2)=logab1+logab2.
Lôgarit của một tích bằng tổng các lôgarit.
Chứng minh. Đặt α1=logab1,α2=logab2, ta có
α1+α2=logab1+logab2 (1)
Mặt khác, vì b1=aα1,b2=aα2, suy ra b1b2=aα1.aα2=aα1+α2
Do đó α1+α2=loga(b1b2) (2)
Từ (1), (2) suy ra
loga(b1b2)=logab1+logab2
Lôgarit của một phương
Định lý 2: Cho ba số dương a,b1,b2 với a≠1, ta có
logab1b2=logab1–logab2
Lôgarit của một thương bằng hiệu các lôgarit.
Định lý 2 được chứng minh tương tự Định lí 1.
Lôgarit của một lũy thừa
Định lí 3: Cho hai số dương a,b;a≠1. Với mọi α, ta có logabα=αlogab.
Lôgarit của một lũy thừa bằng tích của số mũ với lôgarit của cơ số.
Đặc biệt: logab√n=1nlogab
Chứng minh. Đặt β=logab thì b=aβ
Do đó: bα=(aβ)α=aαβ
Suy ra αβ=logabα hay αlogab=logabα
Đổi cơ số :
Định lí 4: Cho ba số dương a, b, c với a≠1,c≠1, ta có logab=logcblogca
Đặc biệt logab=1logba (b ≠ 1)
logaαb=1αlogab (a ≠ 0)
Chứng minh. Theo tính chất của Lôgarit và định lí 3, ta có
logcb=logc(alogab)=logab.logca
Vì a≠1 nên logca≠0. Do đó
logab= logcb/logca
Cách học thuộc công thức lôgarit nhanh nhất
1. Công thức “bay”
Công thức (1) được gọi là “bay trên”, công thức (2) là “bay dưới”, công thức (3) là “bay đúp”.
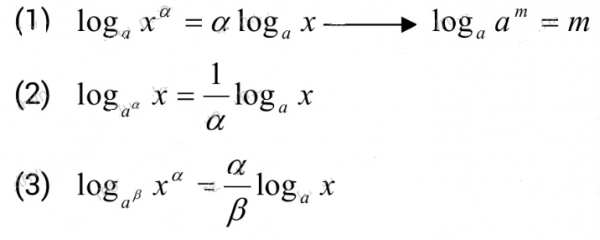
2. Công thức “bỏ”
Công thức (4) thật ra là một tính chất của hàm số lôgarit, được dùng nhiều trong việc giải phương trình lôgarit.
Công thức (5), (6) là công thức đổi cơ số và hệ quả. Bạn đọc dễ thấy được “quy tắc lược bỏ” trong các công thức này.
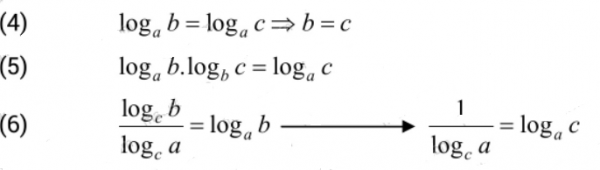
Công thức “đội đầu”
Đây thực ra là định nghĩa lôgarit.
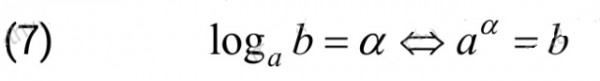
Công thức “độn thổ”
Khi c “độn thổ” thì đẩy a lên trên.
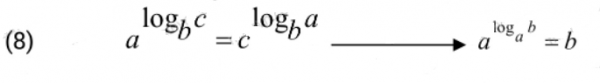
Tích tổng – Thương hiệu
Lôgararit của tích bằng tổng các lôgarit, lôgarit của thương bằng hiệu các lôgarit (theo thứ tự).
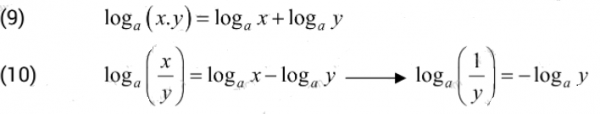
Nội dung xem thêm :

