Mỗi dạng bài toán có một cách và phương pháp giải khác nhau, cũng như hàm số mũ thì hàm số lôgarít có tập giá trị và phương pháp giải phù hợp với bài toán. Ở bài này chúng tôi sẽ hướng dẫn các bạn cách tìm Tập giá trị của hàm số logarit và Bài tập vận dụng để có thể làm các bài toán từ dễ đến khó khác nhau. Mời các bạn cùng theo dõi.
Định nghĩa :
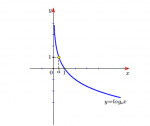
Hàm số lôgarit là hàm số có dạng y=logax ( với cơ số a dương khác 1).
Tính chất của hàm số lôgarit y=logax (a>0,a≠1).
– Tập xác định: (0;+∞).
–Tập giá trị T=R nghĩa là khi giải phương trình logarit mà đặt t= logax thì t không có điều kiện.
Chú ý :
- Hàm số lôgarít là gì? Khảo sát và phân dạng hàm số lôgarít
- Khái niệm hàm số mũ là gì? Tính chất và Đạo hàm của hàm số mũ
- Quy tắc tính, Cách học thuộc công thức Lôgarit nhanh nhất
– Đạo hàm ∀x∈(0;+∞) 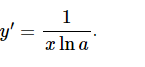
– Chiều biến thiên:
+) Nếu a>1 thì hàm số luôn đồng biến
+) Nếu 0<a<1 thì hàm số luôn nghịch biến
– Tiệm cận: Trục Oy là tiệm cận đứng
.- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).
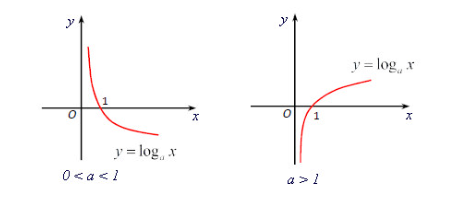
Chú ý
– Nếu a>1 thì lna>0, suy ra (ax)′>0∀x và (logax)>0,∀x>0;
do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.
Tương tự, nếu 0<a<1 thì lna<0, (ax)′<0 và (logax)<0,∀x>0;
hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến
.- Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành
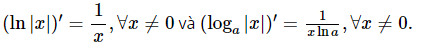
Xem thêm :
- Bảng tóm tắt công thức Lôgarit và bài tập vận dụng
- Định nghĩa Lôgarit là gì? Tính chất và Các đồng nhất thức logarit
Bài tập vận dụng:
Bài 1 : Tìm tập xác định của hàm số y=(x^2-16)^-5-ln(24-5x-x^2).
Bài làm:
Tập xác định của hàm số y = (x2-16)-5 – ln(24-5x-x2)là:
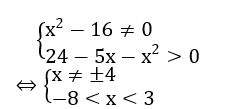
Vậy tập xác định là : D=(-8;3)\{-4}.
Bài 2 :
Tìm tập xác định của hàm số 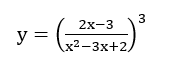
Bài làm :
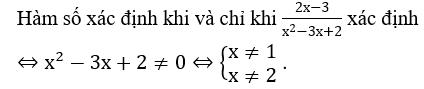
Bài 3 :
Tìm tập xác định D của hàm số
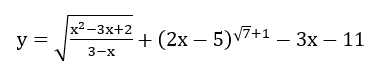
Bài làm :
Hàm số xác định khi và chỉ khi
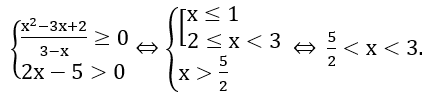
Vậy tập xác định của hàm số là D=(5/2; 3).