Chúng ta đã biết được tầm quan trọng của hàm số lũy thừa ở các dạng bài tập như thế nào? Hàm số mũ cũng thế. Vậy bạn đã tìm hiểu xem Khái niệm hàm số mũ là gì? Tính chất và Đạo hàm của hàm số mũ là gì chưa? Ở bài viết dưới đây chúng ta sẽ cùng nhau đi tìm hiểu rõ về hàm số mũ như thế nào nhé.
Khái niệm hàm số mũ là gì?
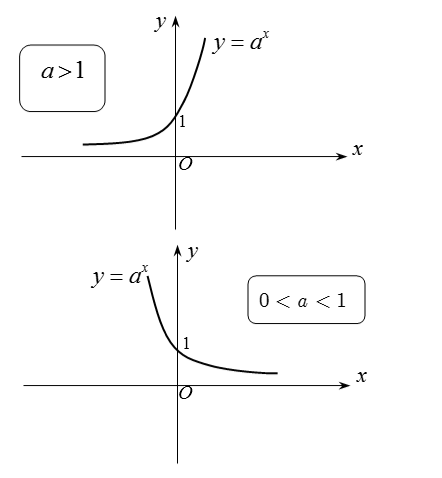
Hàm số mũ : y = ax, (a > 0, a ≠ 1)
1.1 Tập xác định: D = R
1.2. Tập giá trị: T = (); +∝), nghĩa là khi giải phương trình mũ mà đặt t = af(x) thì t > 0
1.3. Tính đơn điệu:
+ Khi a > 1 thì hàm số y = ax đồng biến, khi đó ta luôn có: af(x) > ag(x) ⇔ f(x) > g(x).
+ Khi 0 < a < 1 thì hàm số y = ax nghịch biến, khi đó ta luôn có: af(x) > ag(x) ⇔ f(x) < g(x).
Đạo hàm:
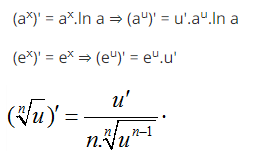
Đồ thị: Nhận trục hoành làm đường tiệm cận ngang.
Xem thêm tại đây :
- Quy tắc tính, Cách học thuộc công thức Lôgarit nhanh nhất
- Bảng tóm tắt công thức Lôgarit và bài tập vận dụng
- Cách tính lũy thừa trên máy tính casio fx 500ms
Một số dạng toán thường gặp
Dạng 1: Tìm hàm số có đồ thị cho trước và ngược lại.
Phương pháp:
– Bước 1: Quan sát dáng đồ thị, tính đơn điệu,…của các đồ thị bài cho.
– Bước 2: Đối chiếu với hàm số bài cho và chọn kết luận.
Dạng 2: Tìm mối quan hệ giữa các cơ số khi biết đồ thị.
Phương pháp:
– Bước 1: Quan sát các đồ thị, nhận xét về tính đơn điệu để nhận xét các cơ số.
+ Hàm số đồng biến thì cơ số lớn hơn 1.
+ Hàm số nghịch biến thì cơ số lớn hơn 0 và nhỏ hơn 1.
– Bước 2: So sánh các cơ số dựa vào phần đồ thị của hàm số.
– Bước 3: Kết hợp các điều kiện ở trên ta được mối quan hệ cần tìm.
Đối với một số bài toán phức tạp hơn thì ta cần chú ý thêm đến một số yếu tố khác như điểm đi qua, tính đối xứng,…
Dạng 3: Tính đạo hàm các hàm số.
Phương pháp:
– Bước 1: Áp dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương để tính đạo hàm hàm số đã cho.
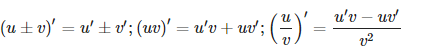
– Bước 2: Tính đạo hàm các hàm số thành phần dựa vào công thức tính đạo hàm các hàm số cơ bản: hàm đa thức, phân thức, hàm mũ, logarit, lũy thừa,…
– Bước 3: Tính toán và kết luận.
Dạng 4: Tính giới hạn các hàm số.
Phương pháp:
Áp dụng các công thức tính giới hạn đặc biệt để tính toán:
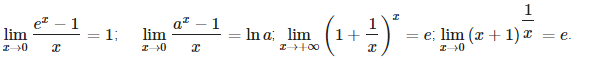
Dạng 5: Tìm GTLN, GTNN của hàm số mũ trên một đoạn.
Phương pháp:
– Bước 1: Tính y′, tìm các nghiệm x1,x2,…,xn∈[a;b] của phương trình y′=0.
– Bước 2: Tính f(a),f(b),f(x1),…,f(xn).
– Bước 3: So sánh các giá trị vừa tính ở trên và kết luận GTLN, GTNN của hàm số.
+ GTNN m là số nhỏ nhất trong các giá trị tính được.
+ GTLN M là số lớn nhất trong các giá trị tính được.
Nội dung tham khảo :