Ở những bài trước chúng ta đã đi tìm hiểu sâu về Lũy thừa, Công thức và định nghĩa của lũy thừa. Bài này chúng ta cùng nhau đi tìm hiểu thế nào là Lôgarit? Tính chất và Các đồng nhất thức logarit phương pháp giải bài toán như thế nào? Mời các bạn và các em học sinh cùng tìm hiểu.
Phép cộng, phép nhân và lũy thừa là ba trong các phép toán số học cơ bản nhất. Phép toán ngược lại với phép cộng là phép trừ, ngược lại với phép nhân là phép chia. Một cách tương tự, logarit là phép toán ngược lại với lũy thừa. Lũy thừa tức là khi một số b, gọi là cơ số, được nâng lên lũy thừa y, gọi là số mũ, để cho giá trị x.
Logarit cơ số b chính là phép toán ngược, cho giá trị là y từ một số x ban đầu. Có nghĩa là, y = logb x tương đương với x = by với b là số thực dương. (Nếu b không phải là số thực dương, phép lũy thừa và logarit vẫn xác định nhưng có thể cho các giá trị khác nhau, dẫn đến việc định nghĩa phức tạp hơn.)
Định nghĩa:
Cho hai số dương a, b với a ≠ 1 . Số α thỏa mãn đẳng thức aα = b được gọi là lôgarit cơ số a của b và kí hiệu là logab. Ta viết: α = logab ⇔ aα = b.
Xem thêm tại đây :
- Cách tính lũy thừa trên máy tính casio fx 500ms
- Chuyên đề : Toán lũy thừa lớp 7 nâng cao
- Cách tính lũy thừa với số mũ âm Toán học 6
Các tính chất:
Cho a, b > 0, a ≠ 1 ta có:
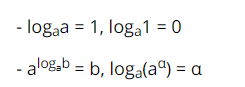
Ví dụ
Ta có log2 16 = 4 vì 24 = 2 × 2 × 2 × 2 = 16. Logarit có thể là số âm:
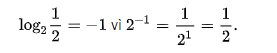
Một ví dụ khác: log10150 gần bằng 2,176, một số nằm giữa 2 và 3, giống như khi 150 nằm giữa 102 = 100 và 103 = 1000. Cuối cùng, với mọi cơ số b thì logb b = 1 và logb 1 = 0 vì b1 = b và b0 = 1.
Các đồng nhất thức logarit
Logarit của một tích là tổng các logarit của các thừa số; logarit của một thương gồm hai số là hiệu logarit của hai số đó. Logarit của một số lũy thừa p bằng p lần logarit của số đó; logarit của một số căn bậc p là logarit của số đó chia cho p. Bảng dưới đây liệt kê các phép tính logarit cơ bản nêu trên và các ví dụ.

Công thức đổi cơ số: Cho 3 số dương a, b, c với a ≠ 1, c ≠ 1 , ta có
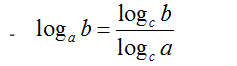
– Đặc biệt : 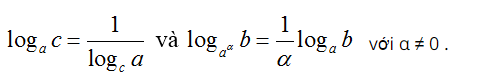
+ Lôgarit thập phân và Lôgarit tự nhiên
+ Lôgarit thập phân là lôgarit cơ số 10. Viết: log10b = log b = lg b
+ Lôgarit tự nhiên là lôgarit cơ số e. Viết: logeb = ln b
Chú ý :
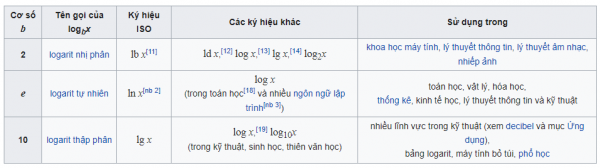
Các cơ số đặc biệt:
Trong các giá trị của cơ số b, có ba cơ số đặc biệt. Chúng gồm b = 10, b = e (hằng số vô tỉ xấp xỉ bằng 2,71828) và b = 2. Trong giải tích toán học, logarit cơ số e là phổ biến nhất nhờ các tính chất được giải thích dưới đây. Mặt khác, có thể dễ dàng tính logarit cơ số 10 trong hệ thập phân:![]()
Do đó, log10x có liên hệ với số chữ số của một số nguyên dương x: đó là số nguyên nhỏ nhất lớn hơn log10x
Bảng dưới đây liệt kê các ký hiệu logarit thông dụng và lĩnh vực mà chúng được sử dụng. Một số tài liệu viết logx thay vì logbx khi cơ số của logarit là cố định tùy theo trường hợp. Ký hiệu blogx cũng tồn tại.[9] Cột “Ký hiệu ISO” liệt kê các ký hiệu do Tổ chức tiêu chuẩn hóa quốc tế khuyến nghị (ISO 80000-2).