Để tìm cực trị hàm số toán cao cấp một cách khái quát nhất thì chúng ta phải hiểu được định nghĩa, điều kiện và quy tắc nhất định của bài toán để giải nhanh nhất có thể. Sau đây chúng tôi sẽ giới thiệu đến các bạn nội dung cũng như bài tập vận dụng để các em nắm được.
Chứng minh, điều kiện hai đường thẳng song song
Cộng trừ, rút gọn đơn thức và cộng trừ đơn thức đồng dạng
Cách tìm cực trị của hàm số
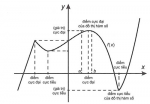
1.Định nghĩa: Cho hàm số y = f(x)xác định và liên tục trên khoảng (a;b) (có thể a là -; b là +) và điểm x0(a;b).
Nếu tồn tại số h > 0 sao cho f(x)< f(x0 ) với mọi x (x0 – h;x0 + h) và xx_0 thì ta nói hàm số f(x) đạt cực đại tại x0.
Nếu tồn tại số h >0 sao cho f(x) >f(x0 ) với mọi x (x0 – h;x0 + h) và x x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.
2.Quy tắc tìm cực trị của hàm số
Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
- [ Tính chất đường cao trong tam giác ] vuông, cân, đều lớp 7.
- Công thức tính thể tích khối lập phương – V khối lập phương.
Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x). Giải phương trình f'(x)và ký hiệuxi (i=1,2,3,…)là các nghiệm của nó.
Bước 3. Tính f”(x) và f”(xi ) .
Bước 4. Dựa vào dấu của f”(xi )suy ra tính chất cực trị của điểm xi.
3.Điều kiện đủ để hàm số có cực trị: Giả sử hàm số y=f(x) liên tục trên
K=(x0 – h;x0 + h)và có đạo hàm trên K hoặc trên K\{x0}, với h >0.
Nếu f'(x)> 0 trên khoảng (x0 – h;x0) và f'(x) <0 trên (x0;x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
Nếu f'(x) < 0 trên khoảng (x0 – h;x0) và f'(x) >0 trên (x0;x0+ h) thì x0 là một điểm cực tiểu của hàm số f(x).
Nếu hàm sốy=f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCÑ (fCT), còn điểm M(x0;f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
Bài tập 1 :
Tìm cực trị của hàm số y = x4 – 2×2 + 2.
Hướng dẫn
Tập xác định D = R.
Tính y’ = 4×3 – 4x. Cho y’= 0 4×3 – 4x = 0
x=0
x=+_1
Bảng biến thiên
Vậy hàm số đạt cực tiểu tại x = ±1, y = 1 và hàm số đạt cực đại tại x = 0, y = 2.
Tìm tham số m để hàm số đạt cực trị tại một điểm
Trong dạng toán này ta chỉ xét trường hợp hàm số có đạo hàm tại x0.
Khi đó để giải bài toán này, ta tiến hành theo hai bước.
Bước 1. Điều kiện cần để hàm số đạt cực trị tại x0 là y'(x0) = 0, từ điều kiện này ta tìm được giá trị của tham số .
Bước 2. Kiểm lại bằng cách dùng một trong hai quy tắc tìm cực trị ,để xét xem giá trị của tham số vừa tìm được có thỏa mãn yêu cầu của bài toán hay không?
Biện luận theo m số cực trị của hàm số
1. Cực trị của hàm số bậc ba
Cho hàm số y = ax3 + bx2 + cx + d, a 0.
y’ = 0 3ax2 + 2bx + c = 0 (1) ; Δ’y’ = b2 – 3ac
Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
Hàm số bậc 3 không có cực trị b2 – 3ac 0
Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
Hàm số bậc 3 có 2 cực trị b2 – 3ac > 0
2. Cực trị của hàm số bậc bốn trùng phương
Cho hàm số: y = ax4 + bx2 + c (a 0) có đồ thị là (C).
y’ = 4ax3 + 2bx; y’ = 0
(C)có một điểm cực trị y’ = 0 có 1 nghiệm x = 0 -b/2a 0 ab 0.
(C)có ba điểm cực trị y’ = 0 có 3 nghiệm phân biệt -b/2a > 0 ab < 0.
Ví dụ áp dụng:
Ví dụ 1: Tìm m để hàm số y = x3 + mx + 2 có cả cực đại và cực tiểu.
Hướng dẫn
y’ = 3×2 + m.
Hàm số y = x3 + mx + 2 có cả cực đại và cực tiểu khi và chỉ khi y’= 0 có hai nghiệm phân biệt.
Vậy m < 0.
Ví dụ 2:
Tìm m để hàm số y = x4 – 2(m + 1)x2 – 2m – 1 đạt cực đại tại x = 1 .
Hướng dẫn
Tập xác định D = R.
Ta có y’ = 4×3 -4(m + 1)x.
+ Để hàm số đạt cực đại tại x = 1 cần y'(1) = 0 4 – 4(m + 1) = 0 m = 0
+ Với m = 0 y’ = 4×3 – 4x y'(1) = 0.
+ Lại có y” = 12×2 – 4 y”(1) = 8 > 0.
Hàm số đạt cực tiểu tại x = 1 m = 0 không thỏa mãn.
Vậy không có giá trị nào của m để hàm số đạt cực đại tại x = 1.
Xem thêm tại đây :
Chuyên đề cực trị của hàm số lớp 12 và Bài tập vận dụng
Bảng đơn vị đo diện tích – Đổi đơn vị đo diện tích mét vuông lớp 4.
7 hằng đẳng thức đáng nhớ có phát biểu bằng lời dễ học lớp 7 ,8 , 9.