Tính chất đường cao trong tam giác rất quan trọng đối với học sinh, vì vậy để làm được các bài tập dạng này anh chị cần lắm kỹ lý thuyết tính chất đường cao trong tam giác vuông, cân, đều và tính chất ba đường cao của tam giác sẽ được chúng tôi giới thiệu đầy đủ ở trong bài học hôm nay.
- Xem thêm : Tính chất đường trung tuyến trong tam giác
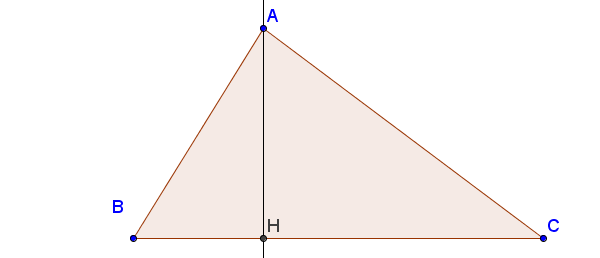
Tính chất đường cao trong tam giác là gì?
Đường cao trong tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được gọi là đáy ứng với đường cao. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy. Mỗi tam giác có ba đường cao.
Tính chất ba đường cao của tam giác
Định lý: Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác
Tính chất đường cao trong tam giác vuông
Cho hình vẽ sau và chứng minh tính chất đường cao trong tam giác vuông
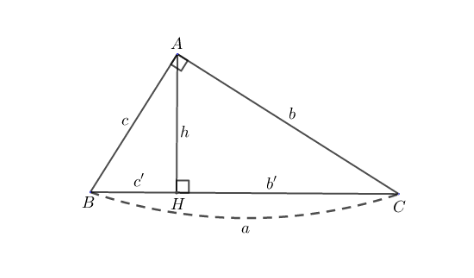
Định lý 1 : Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạng góc vuông đó tên cạnh huyền.
Giả thiết như sau :
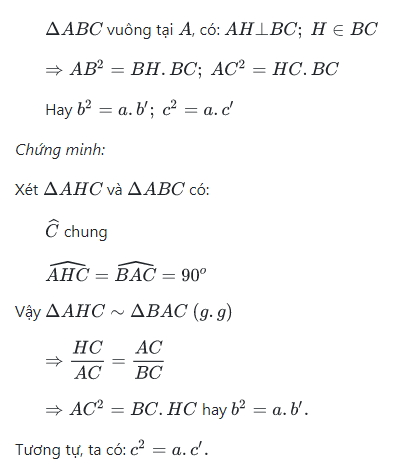
Kết luận : Trong một tam giác vuông, mỗi cạnh góc vuông là trung bình nhân của cạnh huyền và hình chiếu của cạnh góc vuông đó là trên cạnh huyền.
Định lý 2 : Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền
Giả sử
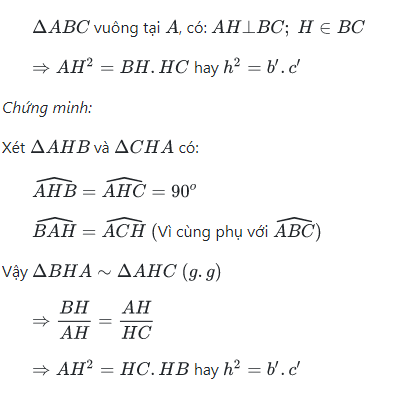
Kết luận : Trong một tam giác vuông, đường cao ứng với cạnh huyền là trung bình nhân của 2 đoạn thẳng mà nó định ra trên cạnh huyền
Định lý 3 : Trong một tam giác vuông, tích 2 cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng


Định lý 4 : Trong một tam giác vuông, nghịc đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương 2 cạnh góc vuông
Giả sử:
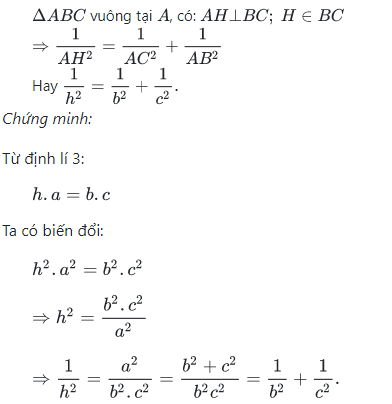
Tính chất đường cao trong tam giác cân
- Trong tam giác cân có 2 góc ở đáy bằng nhau
- Nếu một tam giác có 2 góc bằng nhau thì là tam giác cân
- Tam giác vuông cân là tam giác vuông có 2 cạnh góc vuông bằng nhau.
Tính chất đường cao trong tam giác đều
- Đường cao trong tam giác đều cũng chính là đoạn thẳng kẻ từ đỉnh của tam giác vuông góc với cạnh đáy.
- Độ dài của đường cao chính là độ dài của đường thẳng đó.
- Trong một tam giác đều sẽ có 3 đường cao tương ứng kẻ từ 3 đỉnh của tam giác tới các cạnh đáy.
- Đường cao trong tam giác đều chính là đường trung trực của cạnh đáy và cũng chính là đường phân giác của ở đỉnh tam giác và cũng chính là đường trung tuyến.
- Đường cao trong tam giác đi qua trung điểm của cạnh đáy, vuông góc với cạnh đáy và chia cạnh đáy thành 2 phần bằng nhau.
- Đường cao của tam giác đều chia góc ở đỉnh thành 2 góc có số đo bằng nhau, đều bằng 1/2 60º = 30º.
- Một đường cao trong tam giác đều sẽ chia tam giác đó thành 2 tam giác vuông bằng nhau.