Ở chương trình học THCS lớp 7,8,9 để học tốt môn toán thì việc học thuộc lòng 7 hằng đẳng thức đáng nhớ là điều vô cùng quan trọng . Chính vì vậy các bạn nên học thuộc lòng , ôn tập liên tục hằng đẳng thức để áp dụng vào trong bài tập toán nhanh và chính xác nhất .
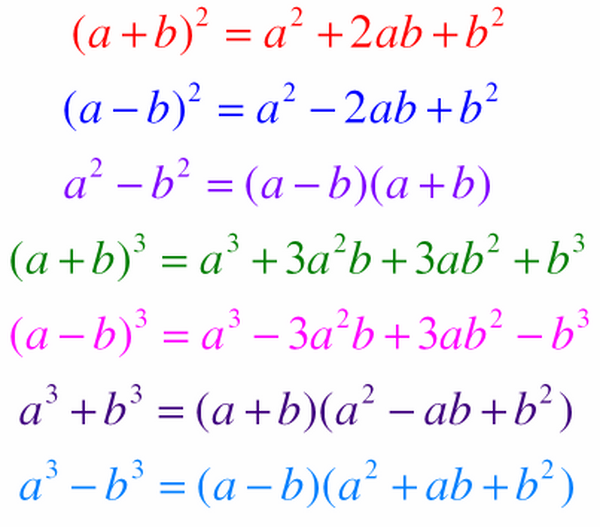
7 hằng đẳng thức đáng nhớ
Bình phương của một tổng : ( a + b )² = a² + 2ab + b²
Bình phương của một hiệu : ( a – b )² = a² – 2ab + b²
Hiệu hai bình phương : a² – b² = ( a + b ) (a – b )
Lập phương của một tổng : ( a + b )³ = a³ + 3a²b + 3ab² + b³
Lập phương của một hiệu : ( a – b )³ = a³ – 3a²b + 3ab² – b³
Tổng hai lập phương : a³ + b³ = ( a + b ) ( a² – ab + b² )
Hiệu hai lập phương : a³ – b³ = ( a – b ) ( a² + ab + b² )
Phát biểu bẩy hằng đẳng thức đáng nhớ bằng lời
- Bình phương của 1 tổng sẽ bằng bình phương của số thứ 1 cộng với hai lần tích của số thứ nhất với số thứ hai cộng bình phương số thứ hai
- Bình phương của 1 hiệu sẽ bằng bình phương của số thứ 1 trừ 2 lần tích số thứ nhất với số thứ 2 cộng với bình phương số thứ 2.
- Hiệu của 2 bình phương sẽ bằng tích của tổng 2 số với hiệu 2 số.
- Lập phương của 1 tổng sẽ bằng với lập phương số thứ 1 + 3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 + lập phương số thứ 2.
- Lập phương của 1 tổng sẽ bằng với lập phương số thứ 1 -3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 – lập phương số thứ 2.
- Tổng hai lập phương sẽ bằng tích giữa tổng 2 số với bình phương thiếu của 1 hiệu.
- Hiệu của 2 lập phương sẽ bằng với tích giữa hiệu hai số với bình phương thiếu của 1 tổng.
1. Bình phương của một tổng
(a + b)² = a² + 2ab + b²
- Bình phương của một tổng bằng bình phương của số thứ nhất cộng với hai lần tích của số thứ nhất nhân với số thứ hai, cộng với bình phương của số thứ hai
2. Bình phương của một hiệu
(a – b)² = a² – 2ab + b²
- Bình phương của một hiệu bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất nhân số thứ hai sau đó cộng bình phương với số thứ hai.
3. Hiệu hai bình phương
a² – b² = (a – b)(a + b)
- Hiệu hai bình phương của hai số bằng tổng hai số đó nhân với hiệu hai số đó.
4. Lập phương của một tổng
(a + b)³ = A³ + 3a²b + 3ab² + b³
- Lập phương của một tổng hai số bằng lập phương của số thứ nhất cộng với ba lần tích bình phương số thứ nhất nhân số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai cộng với lập phương số thứ hai.
5. Lập phương của một hiệu
(a – b)³ = a³ – 3a²b + 3ab² – b³
- Lập phương của một hiệu hai số bằng lập phương của số thứ nhất trừ đi ba lần tích bình phương của số thứ nhất nhân với số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai trừ đi lập phương số thứ hai
6. Tổng hai lập phương
a³ + b³ = (a + b)(a² – ab + b² )
- Tổng của hai lập phương hai số bằng tổng của hai số đó nhân với bình phương thiếu của hiệu hai số đó
7. Hiệu hai lập phương
a³ – b³ = (a – b)(a² + ab + b²)
- Hiệu của hai lập phương của hai số bằng hiệu hai số đó nhân với bình phương thiếu của tổng của hai số đó.
Hằng đẳng thức mở rộng
Hằng đẳng thức đáng nhớ với hàm bậc 2
( a + b + c )² = a² + b² + c² + 2ab + 2ac + 2bc
( a + b – c )² = a² + b² + c² + 2ab – 2ac – 2bc
( a – b – c )² = a² + b² + c² – 2ab – 2ac + 2bc
Hằng đẳng thức đáng nhớ với hàm bậc 3
a³ + b³ = ( a + b )³ – 3ab( a + b)
a³ – b³ = ( a – b )³ + 3ab( a – b )
( a + b + c )³ = a³ + b³ + c³ + 3( a + b )( a + c )( b + c )
a³ + b³ + c³ – 3abc = ( a + b + c )( a² + b² + c² – ab – bc – ac )
( a – b )³ + ( b – c )³ + ( c – a )³ = 3( a – b )( b – c )( c – a )
( a + b )( b + c )( c + a ) – 8abc = a( b – c )² + b( c – a )² + c( a – b )²
( a + b )( b + c )( c + a ) = ( a + b + c ) ( ab + bc + ca ) – abc
Hằng đẳng thức dạng tổng quát .
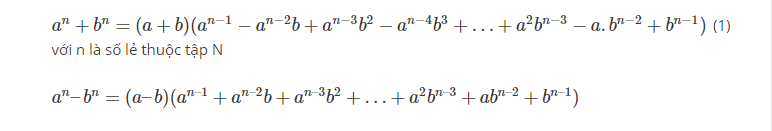
Các dạng bài tập về hằng đẳng thức đáng nhớ
Dạng 1: Tính giá trị của các biểu thức.
Dạng 2: Chứng minh biểu thức a mà không phụ thuộc biến.
Dạng 3: Áp dụng để tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức.
Dạng 4: Chứng minh đẳng thức bằng nhau.
Dạng 5: Chứng minh bất đẳng thức
Dạng 6: Phân tích đa thức thành nhân tử.
Dạng 7: Tìm giá trị của x
Bài tập về hằng đẳng thức đáng nhớ
bài tập 1 : Với a và b là hai số bất kì, thức hiện phép tính (a + b)(a + b).
đáp án
(a + b)(a + b) = a(a + b) + b(a + b)
= a2 + ab + ba + b2
= a2 + 2ab + b2
bài tập 2 : Tính [a + (-b)]2 (với a, b là các số tùy ý).
đáp án
Ta áp dụng hằng đẳng thức 1 ta có như sau
[ a + (-b)]² = a² + 2.a.(-b) + ( -b)² = a² – 2ab + b² .
Ví dụ 3: Tìm giá trị củ x biết: x2( x – 3) – 4x + 12 = 0
đáp án
x² (x – 3) – 4x + 12 = 0
⇔ x² (x – 3) – 4(x – 3) = 0
⇔ (x – 3) (x2 – 4) = 0
⇔ (x – 3)(x – 2)(x + 2) = 0
⇔ (x – 3) = 0 hoặc (x – 2) = 0 hoặc (x + 2) = 0
⇔ x = 3 hoặc x = 2 hoặc x = –2
⇒ Kết luận, vậy nghiệm : x = 3; x = 2; x = –2
Trên đây là toàn bộ kiến thức về 7 hằng đẳng thức đáng nhớ lớp 7,8,9 trong chương trình trung học cơ sở mà các bạn cần lắm được để áp dụng bẩy hằng đẳng thức đáng nhớ vào các dạng bài tập chi tiết nhất.