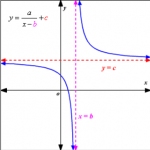
Chúng ta đã đi tìm hiểu định nghĩa đường tiệm cận, công thức tính cũng như các dạng bài tập, ở bài này chúng ta sẽ đi tìm hiểu tiệm cận của đồ thị hàm số và cách giải tiệm cận hàm số bằng máy tính. Hi vọng sẽ giúp các em giải được các bài toán có trong các đề kiểm tra cũng như phần bài tập ở sách giáo khoa có trong chương trình học.
Tiệm cận của đồ thị hàm số:
Cách tìm tiệm cận đứng:
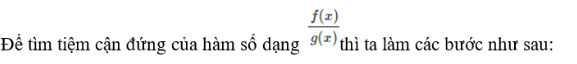
Bước 1: Tìm nghiệm của phương trình g(x) = 0
Bước 2: Trong số những nghiệm tìm được ở bước trên, loại những giá trị là nghiệm của hàm số f(x)
Bước 3: Những nghiệm x0 còn lại thì ta được đường thẳng x = x0 là tiệm cận đứng của hàm số
Cách tìm tiệm cận ngang:
– Cho đồ thị hàm số y = f(x) có tập xác định D.

Công thức tính tiệm cận ngang của hàm phân thức vô tỷ:

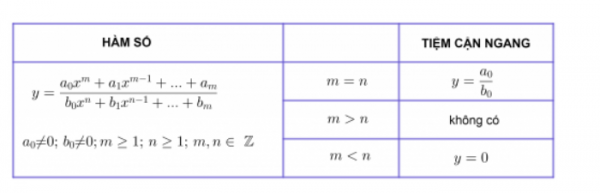
Công thức tính tiệm cận ngang của hàm phân thức hữu tỉ:
Xem thêm :
Đường tiệm cận là gì? Quy tắc tìm đường tiệm cận
Định nghĩa tiệm cận ngang, Công thức tính tiệm cận ngang là gì?
Cách giải tiệm cận bằng máy tính :
Cách tìm tiệm cận đứng bằng máy tính
Để tìm tiệm cận đứng của hàm số dạng f(x) g(x) bằng máy tính thì đầu tiên ta cũng tìm nghiệm của hàm số g(x) rồi sau đó loại những giá trị cũng là nghiệm của hàm số f(x)
– Bước 1: Sử dụng tính năng SOLVE để giải nghiệm. Nếu mẫu số là hàm bậc 2 hoặc bậc 3 thì ta có thể dùng tính năng Equation ( EQN) để tìm nghiệm
– Bước 2: Dùng tính năng CALC để thử những nghiệm tìm được có là nghiệm của tử số hay không.
– Bước 3: Những giá trị x0 là nghiệm của mẫu số nhưng không là nghiệm của tử số thì đường thẳng x=x0 là tiệm cận đứng của hàm số.
Cách tìm tiệm cận ngang bằng máy tính
Để tìm tiệm cận ngang bằng máy tính, chúng ta sẽ tính gần đúng giá trị của limx→+∞y và limx→−∞y.
Để tính limx→+∞y thì chúng ta tính giá trị của hàm số tại một giá trị x rất lớn. Ta thường lấy x=109. Kết quả là giá trị gần đúng của limx→+∞y
Tương tự, để tính limx→−∞y thì chúng ta tính giá trị của hàm số tại một giá trị x rất nhỏ. Ta thường lấy x=−109. Kết quả là giá trị gần đúng của limx→−∞y
Để tính giá trị hàm số tại một giá trị của x , ta dung chức năng CALC trên máy tính.
Chú ý :
Giải bài tập cực trị của hàm số Toán học 12 – Bài 2
Tìm cực trị bằng máy tính cầm tay Fx 580
Tìm cực trị của hàm số toán cao cấp và bài tập
Bài tập áp dụng :
Bài 1 : Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau
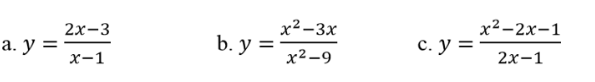
Bài làm:


Bài 2 :Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau
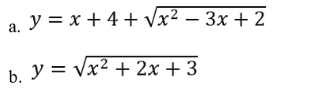
Bài làm
a, Đồ thị hàm số không có tiệm cận đứng