Ở bài 2 toán học lớp 12 chúng ta đã cùng nhau đi tìm hiểu được các định nghĩa, Định lý, công thức hàm trị của cực số. Vậy giải bài tập cực trị của hàm số như thế nào cho chính xác và hiệu quả nhất thì ở dưới bài viết này chúng tôi sẽ đưa ra các dạng bài tập toán khác nhau để các bạn có thể vận dụng một cách chính xác và hiệu quả nhất để giải các bài tập cơ bản cũng như có trong các đề thi quốc gia.
Xem thêm tại đây :
Công thức giải nhanh cực trị hàm bậc 3 của hàm số
Chuyên đề cực trị của hàm số lớp 12 và Bài tập
Tìm cực trị của hàm số toán cao cấp và bài tập
Cực trị của hàm số là gì ?
Cho hàm số y=f(x) liên tục trên khoảng (a;b) và điểm x0∈(a;b)
.- Nếu tồn tại số h>0 sao cho f(x)<f(x0),∀x∈(x0−h;x0+h),x≠x0 thì ta nói hàm số f đạt cực đại tại x0
.- Nếu tồn tại số h>0 sao cho f(x)>f(x0),∀x∈(x0−h;x0+h),x≠x0 thì ta nói hàm số f đạt cực tiểu tại x0.
Chú ý:
a) Cần phân biệt các các
khái niệm
:- Điểm cực trị x0 của hàm số
.- Giá trị cực trị của hàm số
.- Điểm cực trị (x0;y0) của đồ thị hàm số
.b) Nếu y=f(x) có đạo hàm trên (a;b) và đạt cực trị tại x0∈(a;b) thì f′(x0)=0.
Điều kiện đủ để hàm số có cực trị
Định lí 1. Cho hàm số y=f(x) liên tục trên khoảng K=(x0−h;x0+h)(h>0) và có đạo hàm trên K hoặc trên K∖{x0}
+) Nếu {f′(x)>0|∀(x0−h;x0)
f′(x)<0|∀(x0;x0+h) thì x0 là điểm cực đại của hàm số
+) Nếu {f′(x)<0|∀(x0−h;x0)
f′(x)>0|∀(x0;x0+h) thì x0 là điểm cực tiểu của hàm số
Hàm số có thể đạt cực trị tại những điểm mà tại đó đạo hàm không xác định.
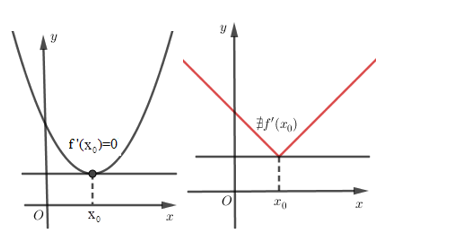
Số điểm cực trị của hàm số, Cực trị hàm tuyệt đối
Tìm cực trị của hàm số, Giá trị cực đại của hàm số
Định lý 2:Giả sử y=f(x) có đạo hàm cấp 2 trong (x0−h;x0+h)(h>0)
a) Nếu {f′(x0)=0
f′′(x0)>0 thì x0 là một điểm cực tiểu của hàm số.
b) Nếu {f′(x0)=0
f′′(x0)<0 thì x0 là một điểm cực đại của hàm số.
Quy tắc tìm cực trị của hàm số
Phương pháp:Có thể tìm cực trị của hàm số bởi một trong hai quy tắc sau:
Quy tắc 1: (suy ra từ định lý 1)
– Bước 1: Tìm tập xác định của hàm số.
– Bước 2: Tính f′(x), tìm các điểm tại đó f′(x)=0 hoặc không xác định.
– Bước 3: Lập bảng biến thiên và kết luận.
+ Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó là điểm cực tiểu của hàm số
.+ Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó là điểm cực đại của hàm số.
Quy tắc 2: (suy ra từ định lý 2)
– Bước 1: Tìm tập xác định của hàm số.
– Bước 2: Tính f′(x), giải phương trình f′(x)=0 và kí hiệu x1,…,xn là các nghiệm của nó.
– Bước 3: Tính f′′(x) và f′′(xi)
.- Bước 4: Dựa và dấu của f′′(xi) suy ra điểm cực đại, cực tiểu:
+ Tại các điểm xi mà f′′(xi)>0 thì đó là điểm cực tiểu của hàm số
.+ Tại các điểm xi mà f′′(xi)<0 thì đó là điểm cực đại của hàm số.
Sơ đồ tư duy công thức lượng giác lớp 10.
Bài tập về cực trị của hàm số:
Bài 1 :
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau :y=2×3+3×2−36x−10 ;
Phương pháp giải:Quy tắc 1 tìm cực trị của hàm số
:Bước 1: Tìm tập xác định
.Bước 2: Tính f′(x). Tìm các điểm mà tại đó f′(x) bằng 0 hoặc f′(x) không xác định
.Bước 3: Lập bảng biến thiên.
Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.
Bài làm :
Tập xác định: D=R
y′=6×2+6x−36;
y′=0
⇔[x=2⇒y=−54
x=−3⇒y=71
y′<0⇔x∈(−3;2)
y′>0⇔x∈(−∞;−3)∪(2;+∞)
limx→−∞y=−∞;
limx→+∞y=+∞
Bảng biến thiên:
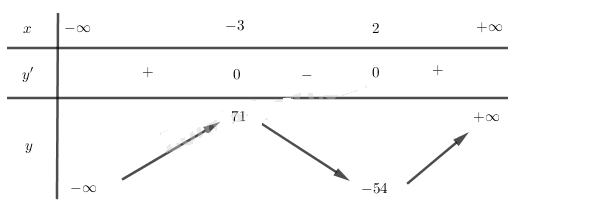
Hàm số đạt cực đại tại x=−3 và yCĐ =71
Hàm số đạt cực tiểu tại x=2 và yCT =−54
Bài 2 :
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau y=x4+2×2−3 ;
Bài làm :
Tập xác định: D=R
y′=4×3+4x=4x(x2+1);
y′=0⇔x=0⇒y=−3
y′>0⇒x>0y′<0⇒x<0
limx→−∞y=+∞;limx→+∞y=+∞
Bảng biến thiên:
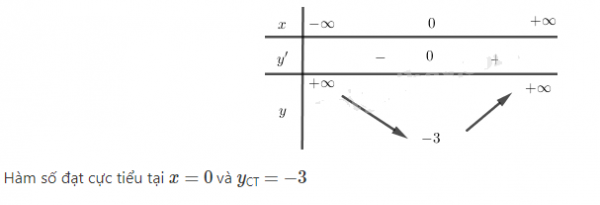
Bài 3 :
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số: f(x)=x(x2−3)
Bài làm
1. TXĐ: D=R2. f(x)=3×2−3. Cho f(x)=0⇔x=1 hoặc x=−1.3.
Ta có bảng biến thiên:
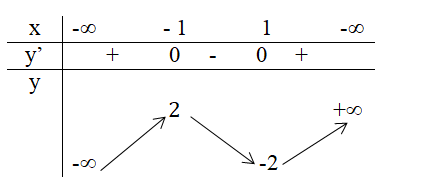
Hàm số đạt cực đại tại x=−1 và giá trị cực đại là 2
Hàm số đạt cực tiểu tại x=1 và giá trị cực tiểu là −2
Bài 4:
a) Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không
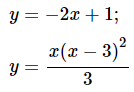
b) Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không
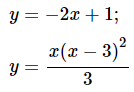
Phương pháp giải:
Quan sát đồ thị, tìm điểm cực trị ( cực đại: điểm mà tại đó hàm số chuyển từ đồng biến sang nghịch biến, cực tiểu: ngược lại)
Lời giải chi tiết
Hàm số y=−2x+1 không có cực trị.
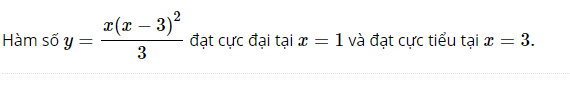
Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
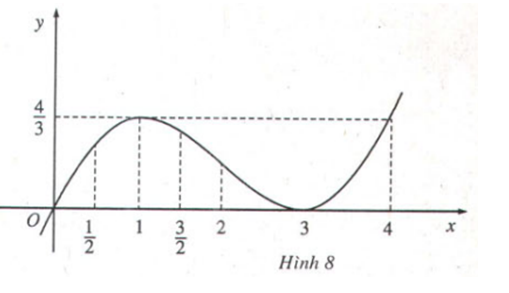
Nếu hàm số có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.