Máy tính casino có rất nhiều công dụng tính toán khác nhau, ở các máy tính đời cao bây giờ có thể giải các bài toán trực tiếp trên máy. Trong bài hôm nay chúng tôi sẽ hướng dẫn chi tiết cho các bạn biết cách tìm cực trị của một hàm số bất kỳ trên máy tính fx-580. Về cơ bản có ba phương pháp, trong đó phương pháp đầu tiên tức phương pháp lập bảng biến thiên là hiệu quả nhất, Riêng đối với hàm số bậc hai và bậc ba thì với các tính năng nguyên thủy là đã tìm được cực trị, không cần thực hiện bất kì thủ thuật nào.
Xem thêm :
Giải bài tập cực trị của hàm số Toán học 12 – Bài 2
Tìm cực trị của hàm số toán cao cấp và bài tập
Cực trị hàm nhiều biến, Cực trị có điều kiện và không điều kiện
Cực trị của hàm số bậc hai:
Chúng ta có thể tìm chính xác cực trị của hàm số bậc hai nhờ vào việc giải phương trình bậc hai tương ứng
Bước 1 Chọn phương tính thức toán Equation/ Func => chọn Polynomial => nhấn phím 2
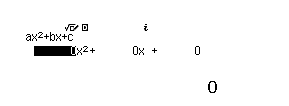
Bước 2 Nhập các hệ số
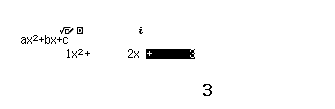
Bước 3 Nhấn phím = chúng ta thu được nghiệm
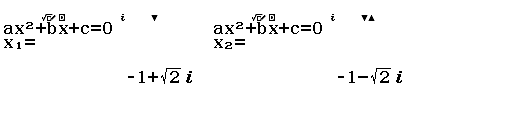
Bước 4 Tiếp tục nhấn phím = chúng ta thu được điểm cực trị
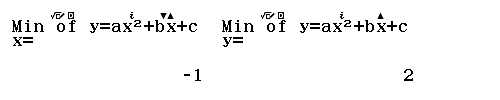
Kết luận
Cách 1 x=-1 là điểm cực tiểu của hàm số và đồ thị hàm số có một điểm cực tiểu là (-1; 2)
Cách 2 f(x) đạt cực tiểu tại x=-1 và f_{CT}=f(-1)=2
Cực trị của một hàm số bất kì
Dựa vào bảng biến thiên
Chi tiết các bước thực hiện bạn vui lòng xem trong bài viết Lập bảng biến thiên bằng máy tính Casio fx-580VN X. Vì mục đích của chúng ta là tìm cực trị của hàm số nên bạn không cần thực hiện Bước 6 trong Thuật giải 1
Tìm điểm cực trị của hàm số 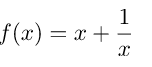
Giải bài tập :
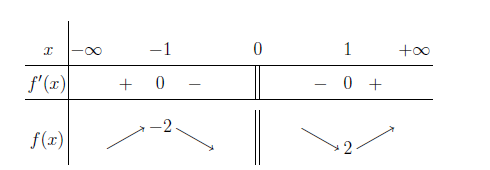
Vậy f(x) đạt cực đại tại x=-1 và f_{CD}=f(-1)=-2, f(x) đạt cực tiểu tại x=1 và f_{CT}=f(1)=2
Dựa vào đạo hàm cấp hai
Tìm điểm cực trị của hàm số 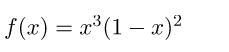
Bước 1 Tìm những điểm làm cho f'(x)=0
Bước 1.1 Giải phương trình 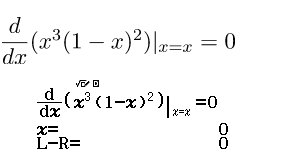
Suy ra x=0 là nghiệm thứ nhất
Bước 1.2 Giải phương trình 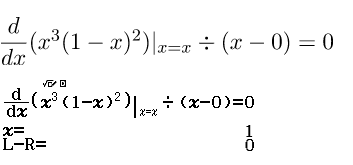
Suy ra x=1 là nghiệm thứ nhì
Bước 1.3 Giải phương trình 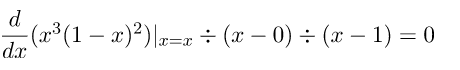
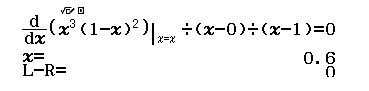
Suy ra x=0.6=3/5 là nghiệm thứ ba
Bước 1.4 Giải phương trình 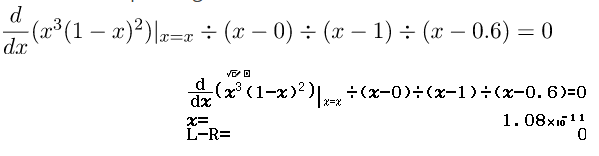

Bước 1.5 Giải phương trình 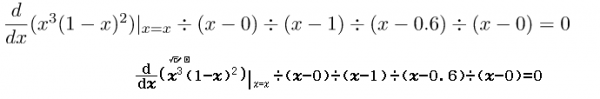
Máy thông báo Cannot Solve tức phương trình
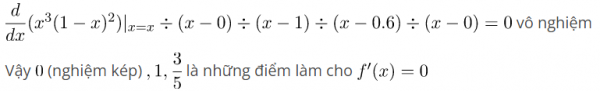
Tìm cực trị của hàm số, Giá trị cực đại của hàm số
Số chẵn số lẻ là gì? Số chẵn là những số nào, số lẻ là những số nào?
Dựa vào phương thức tính toán Table
Phương pháp sử dụng Table thường chỉ khả dụng khi câu hỏi là “Tìm số điểm cực trị của hàm số …” hoặc “Tìm điểm cực trị của hàm số …” với bốn phương án cho trước
Tìm số điểm cực trị của hàm số 
Bước 1 Thiết lập chỉ sử dụng duy nhất hàm f(x)
Bước 2 Chọn phương thức tính toán Table
Bước 3 Nhập biểu thức 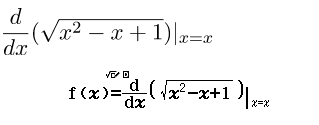
Bước 4 Nhập 
Bước 5 Quan sát bảng giá trị của f(x)
Nếu f(x) < 0 vẽ “dấu huyền”
Nếu f(x) > 0 vẽ “dấu sắc”
Vậy hàm số đã cho có một điểm cực trị (cực tiểu)
Cực trị của hàm số bậc ba
Chúng ta có thể tìm chính xác cực trị của hàm số bậc ba nhờ vào việc giải phương trình bậc ba tương ứng
Tìm điểm cực trị của hàm số ![]()
Bước 1 Chọn phương tính thức toán Equation/ Func => chọn Polynomial => nhấn phím 3
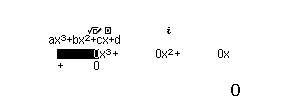
Bước 2 Nhập các hệ số 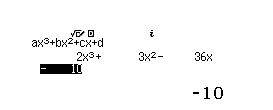
Bước 3 Nhấn phím = chúng ta thu được nghiệm

Bước 4 Tiếp tục nhấn phím = chúng ta thu được các điểm cực trị

Kết luận
Cách 1 x=-3 là điểm cực đại của hàm số và đồ thị hàm số có một điểm cực đại là (-3; 71), x=2 là điểm cực tiểu của hàm số và đồ thị hàm số có một điểm cực tiểu là (2; -54)
Cách 2 f(x) đạt cực đại tại x=-3 và f_{CD}=f(-3)=71, f(x) đạt cực tiểu tại x=2 và f_{CT}=f(2)=-54
Chú ý 2
Nếu hàm số bậc ba không có cực trị thì máy tính sẽ xuất hiện thông báo No Local Max/ Min
Cần phân biệt khái niệm điểm cực trị của hàm số và điểm cực trị của đồ thị hàm số để kết luận cho đúng

