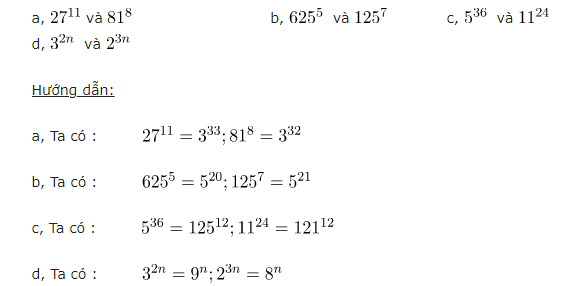Chúng ta đã cùng nhau tìm hiểu khái niệm lũy thừa là gì? Công thức của lũy thừa. Ở bài này chúng ta sẽ cùng nhau đi so sánh hai lũy thừa để xem kết quả và phương pháp giải như thế nào? Các dạng bài tập có liên quan. Hi vọng sẽ giúp các em có được kiến thức quan trọng trong việc giải bài tập.
Xem thêm :
- Định nghĩa lũy thừa là gì? Lũy thừa của lũy thừa, Lũy thừa của một tích
- Công thức tính tổng dãy số lũy thừa toán lớp 6
- Hàm số lũy thừa là gì? Đạo hàm với số mũ tổng quát và khảo sát hàm số
Để so sánh hai luỹ thừa chúng ta có 2 phương pháp để giải bài tập:
Phương pháp 1 :
Ta thường đưa về so sánh hai luỹ thừa cùng cơ số hoặc cùng số mũ:
– Nếu 2 luỹ thừa cùng cơ số ( lớn hơn 1) thì luỹ thừa nào có số mũ lớn hơn sẽ lớn hơn.
Nếu m>n thì a^m>a^n(a>1) ⇔ m > n
– Nếu 2 luỹ thừa cùng số mũ (lớn hơn 0) thì lũy thừa nào có cơ số lớn hơn sẽ lớn hơn .
Nếu a>b thì a^n>b^n(n>0). ⇔ a > b
Phương pháp 2
Dùng tính chất bắc cầu, tính chất đơn điệu của phép nhân:
A > B và B > C thì A > C
A.C < B.C (với C > 0) ⇔ A < B
Để hiểu rõ về các phương pháp trên các em xem ví dụ có lời giải dưới đây.
Chú ý :
- Giá trị lớn nhất và giá trị nhỏ nhất của hàm số – Toán 12
- Chuyên đề cực trị của hàm số lớp 12 và Bài tập vận dụng
Bài tập :
Bài tập 1 :
So sánh hai số (-32)9 và (-16)13
Giải:
Ta có: (-32)9 = -329 (Tính chất lũy thừa với số mũ lẻ)
Suy ra (-32)9 = -329 = -(25)9 = -25.9 = -245
Tương tự: (-16)13 = -1613 = -(24)13 = -24.13 = -252
Vì 0 < 45 < 52 ⇒ 245 < 252 ⇒ -245 > -252 (nhân hai vế với -1)
Vậy (-32)9 < (-16)13.
Bài 2 :
So sánh
a) 2300 và 3200
b) 85 và 3.47
Lời giải:
a) 2300 và 3200
Ta có:
> 2300 = 23.100 = (23)100 = 8100;
> 3200 = 32.100 = (32)100 = 9100
Vì 0 < 8 < 9 nên 8100 < 9100
Vậy 2300 < 3200
b) 85 và 3.47
Ta có:
85 = (23)5 = 23.5 = 215 = 2.214
3.47 = 3.(22)7 = 3.22.7 = 3.214
Vì 2 < 3 nên 2.214 < 3.214 (do 214> 0)
Vậy 85 và 3.47
Bài 3 : so sánh