Các giá trị lớn nhất và giá trị nhỏ nhất của hàm số thường xuyên có trong các bài tập cũng như các đề thi lớp 12 và đề thi quốc gia THPT với các dạng khác nhau. Bài này chúng tôi sẽ giới thiệu về định nghĩa và phương pháp giải của giá trị lớn nhất và giá trị nhỏ nhất của hàm số, Hi vọng sẽ giúp các em nắm được kiến thức cơ bản để giải bài tập hiệu quả nhất.
Định nghĩa
Cho hàm số y=f(x) xác định trên tập D.
– Số M là giá trị lớn nhất (GTLN) của hàm số f trên D⇔{f(x)≤M,∀x∈D∃x0∈D sao cho f(x0)=M Kí hiệu : M=maxD f(x)
.- Số m là giá trị nhỏ nhất (GTNN) của hàm số f trên D⇔{f(x)≥m,∀x∈D∃x0∈D sao cho f(x0)=mKí hiệu: m=minD f(x).
Cách tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn
Định lí
Hàm số liên tục trên một đoạn thì có GTLN và GTNN trên đoạn đó
Quy tắc tìm GTLN, GTNN của hàm số y=f(x) liên tục trên đoạn [a ; b]
– Tìm các điểm xi∈(a;b)(i=1,2,…,n) mà tại đó f′(xi)=0 hoặc f′(xi) không xác định.
– Tính f(a),f(b),f(xi)(i=1,2,…,n).- Khi đó: max[a;b] f(x)=max{f(a);f(b);f(xi)};min[a;b] f(x)=min{f(a);f(b);f(xi)}
Chú ý
Để tìm GTLN, GTNN của hàm số y=f(x) xác định trên tập hợp D, ta có thể khảo sát sự biến thiên của hàm số trên D, rồi căn cứ vào bảng biến thiên của hàm số mà kết luận về GTLN và GTNN của hàm số.
Các dạng bài tập tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Để tìm giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên D ta có thể sử dụng đạo hàm và kết hợp với việc so sánh giá trị cực đại, cực tiểu với giá trị đặc biệt (ta gọi đó là các giá trị tới hạn). Giá trị tới hạn này thường là các giá trị tại các đầu mút của các đoạn hoặc là giá trị của hàm số tại các điểm mà không tồn tại đạo hàm.
Bài 1 :
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x3 – 3×2 – 9x + 2 trên đoạn [-2; 2].
Hướng dẫn giải:
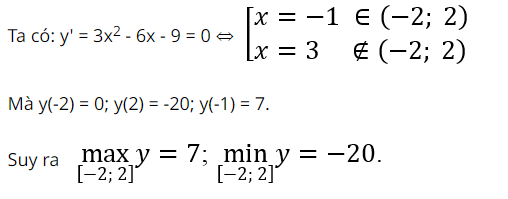
Bài 2 :Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x – sin2x trên đoạn [π/2; π]
Hướng dẫn giải :
Ta có y’ = 1 – 2cos2x = 0 ⇔ cos2x = 1/2 = cos π/3 ⇔ x = ±π/6 + kπ.
Xét x ∈[(-π)/2; π] ta được x = ±π/6; x = 5π/6.
f((-π)/2) = -π/2; f(π) = π; f((-π)/6) = -π/6 + √3/2; f(π/6) = π/6 – √3/2; f(5π/6) = 5π/6 + √3/2.
Suy ra 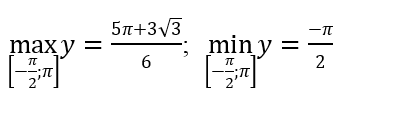
Bài 3 :
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 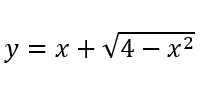
Hướng dẫn giải
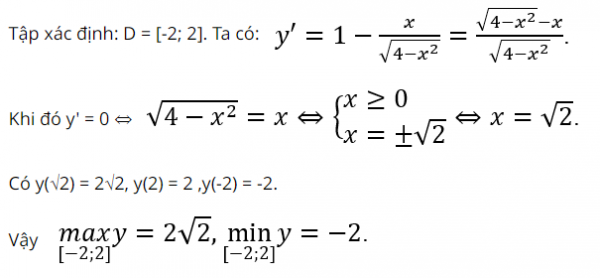
chú ý :