Định nghĩa về lũy thừa là gì? Lũy thừa của lũy thừa là gì? Lũy thừa của một tích. Công thức và các dạng toán liên quan ở trong chương trình học đại số lớp 12 như thế nào? sau bài này chúng ta cùng nhau đi tìm hiểu cụ thể qua bài viết này về lũy thừa nhé.
Định nghĩa về lũy thừa.
Lũy thừa là một phép toán hai ngôi của toán học thực hiện trên hai số a và b, kết quả của phép toán lũy thừa là tích số của phép nhân có b thừa số a nhân với nhau. Lũy thừa ký hiệu là ab, đọc là lũy thừa bậc b của a hay a mũ b, số a gọi là cơ số, số b gọi là số mũ.
Phép toán ngược với phép tính lũy thừa là phép khai căn. Lũy thừa có nghĩa là “nhân chồng chất lên”.
Đặc biệt:
a² còn gọi là “a bình phương”.
a³ còn gọi là “a lập phương”.
Tìm hiểu kiến thức về lũy thừa:
Lũy thừa với số mũ tự nhiên
– Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
an = a.a…..a (n thừa số a) (n khác 0)
– Trong đó: a được gọi là cơ số, n được gọi là số mũ.
Nhân hai lũy thừa cùng cơ số
– Khi nhân hai lũy thừa cùng cơ số, ta giữa nguyên cơ số và cộng các số mũ.
am . an = am+n
Chia hai lũy thừa cùng cơ số
– Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.
am : an = am-n (a ≠ 0, m ≥ 0)
Lũy thừa của lũy thừa
(am )n = am+n
– Ví dụ : (22 )4 = 22.4 = 28
Nhân hai lũy thừa cùng số mũ, khác sơ số
am . bm = (a.b)m
– Ví dụ : 33 . 23 = (3.2)3 = 63
Chia hai lũy thừa cùng số mũ, khác cơ số
am : bm = (a : b)m
– Ví dụ : 64 : 34 = (6 : 3)4 = 24
Một vài quy ước
1n = 1; a0 = 1
– Ví dụ : 12020 = 1 ; 20200 = 1
Lũy thừa của 0 và 1
0m = 0
1m = 1
Chú ý :
- Đường tiệm cận là gì? Quy tắc tìm đường tiệm cận
- Giải bài tập cực trị của hàm số Toán học 12 – Bài 2
1 số tính chất :
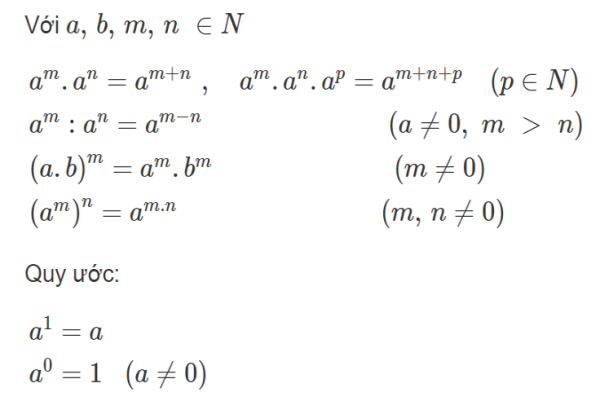
So sánh hai lũy thừa cùng số mũ
Nếu hai luỹ thừa có cùng số mũ (lớn hơn 0) thì luỹ thừa nào có cơ số lớn hơn sẽ lớn hơn:
a > b ⇒ an > bn (n > 0)
Ví dụ: So sánh 45 và 65
Ta thấy 2 số trên có cùng số mũ là 5 và 4 < 6 ⇒ 45 < 65
Ngoài ra, để so sánh hai luỹ thừa ta còn dùng tính chất bắc cầu, tính chất đơn điệu của phép nhân.
a < b thì ac < bc (c>0)
Ví dụ: So sánh 3210 và 1615, số nào lớn hơn.
Ta thấy các cơ số 32 và 16 khác nhau nhưng đều là luỹ thừa của 2 lên ta tìm cách đưa 3210 và 1615 về lũy thừa cùng cơ số 2.
3210 = (25)10 = 250
1615 = (24)15= 260
Vì 250 < 260 ⇒ 3210 < 1615
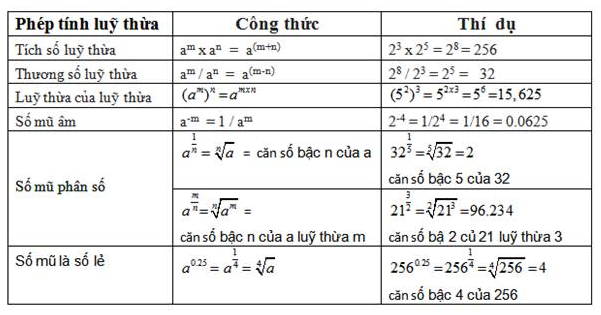
Xem thêm tại đây :

