Ở chương 1 của toán học lớp 12 chúng ta sẽ cùng nhau khảo sát sự biến thiên và vẽ đồ thị của hàm số. Bài viết này chúng ta sẽ điểm qua 3 dạng đồ thị cơ bản nhất gồm: Hàm số bậc 3, hàm phân thức, hàm trùng phương. Mỗi dạng đồ thị sẽ đều có ví dụ và bài tập tự luyện cơ bản để vận dụng làm các bài tập có trong các đề thi tốt nghiệp.Hi vọng giúp được các em học sinh có kiến thức cơ bản nhất.
Xem thêm :
- Tiệm cận của đồ thị hàm số, Cách giải tiệm cận bằng máy tính
- Đường tiệm cận là gì? Quy tắc tìm đường tiệm cận
- Định nghĩa tiệm cận ngang, Công thức tính tiệm cận ngang là gì?
Sơ đồ bài toán khảo sát và vẽ đồ thị hàm số
• Bước 1. Tìm tập xác định của hàm số;
• Bước 2. Tính đạo hàm y’ = f'(x) ;
• Bước 3. Tìm nghiệm của phương trình ;
• Bước 4. Tính giới hạn và tìm tiệm cận đứng, ngang (nếu có);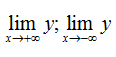
• Bước 5. Lập bảng biến thiên;
• Bước 6. Kết luận tính biến thiên và cực trị (nếu có);
• Bước 7. Tìm các điểm đặc biệt của đồ thị (giao với trục Ox, Oy, các điểm đối xứng, …);
• Bước 8. Vẽ đồ thị.
Khảo sát sự biến thiên hàm số y = ax3 + bx2 + cx + d
1.Tập xác định: D = ℝ
Tính y’ và cho y’ = 0 ⇒ các nghiệm (nếu có)
Tính các giới hạn:
2. Lập bảng biến thiên
Nếu y’ = 0 có hai nghiệm thì dấu của y’ là: “trong trái ngoài cùng”
Nếu y’ = 0 có nghiệm kép thì dấu của y’ là: “luôn cùng dấu với a” ngoại trừ tại nghiệm kép.
Nếu y’ = 0 vô nghiệm thì dấu của y’ là: “luôn cùng dấu với a”
3. Kết luận
Tính chất đơn điệu của hàm số.
Cực trị hàm số
Chọn vài điểm đặc biệt vẽ đồ thị hàm số. Đồ thị có 6 dạng như sau:
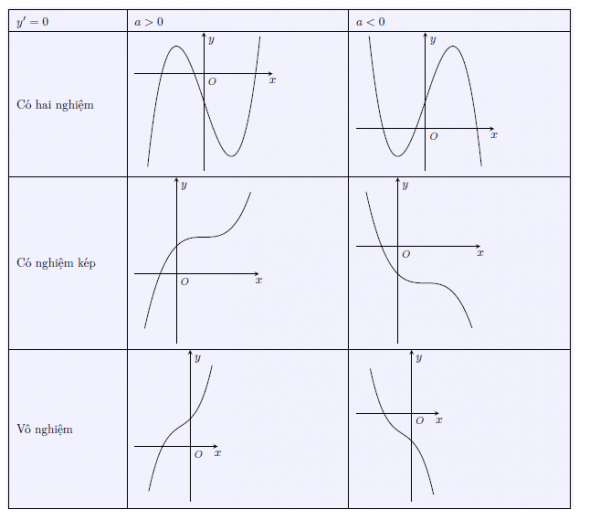
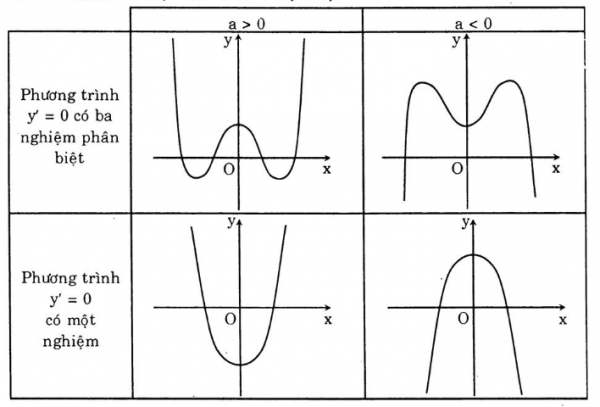
Các dạng đồ thị của hàm số bậc 4 trùng phương y = ax4 + bx2 + c (a ≠ 0)
Tập xác định: D = ℝ
Tính y’ và cho y’ = 0 (có 3 có nghiệm hoặc có 1 nghiệm và luôn có 1 nghiệm x = 0).
Tính giới hạn: 
Lập bảng biến thiên: “Bên phải bảng biến thiên, dấu y’ luôn cùng dấu với a”.
Kết luận:
Tính chất đơn điệu.
Cực trị hàm số.
Giới hạn của hàm số.
Vẽ đồ thị: Chọn vài điểm đặc biệt vẽ đồ thị hàm số
Đồ thị hàm số có 4 dạng sau:
Chú ý :
- Công thức giải nhanh cực trị hàm bậc 3 của hàm số
- Chuyên đề cực trị của hàm số lớp 12 và Bài tập vận dụng
Các dạng đồ thị của hàm số nhất biến (ab – bc ≠ 0)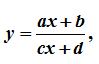
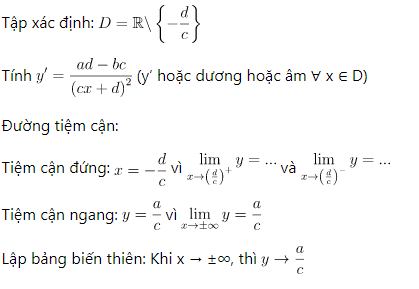
Kết luận:
Hàm số luôn đồng biến trên từng khoảng xác định hoặc luôn nghịch biến trên từng khoảng xác định.
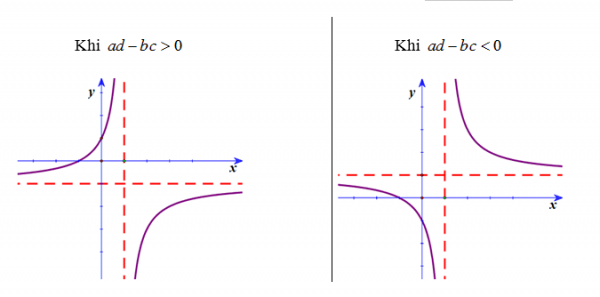
Vẽ đồ thị: Đồ thị có 2 dạng và luôn luôn nhận giao điểm của hai đường tiệm cận là tâm đối xứng.
Vẽ đồ thị: Lấy thêm vài điểm đặc biệt.
Đồ thị có 2 dạng sau:
Biến đổi đồ thị
Cho hàm số y = f(x) có đồ thị (C) . Khi đó, với số a > 0 ta có:
• Hàm số y = f(x) + a có đồ thị (C’) là tịnh tiến (C) theo phương của Oy lên trên a đơn vị.
• Hàm số y = f(x) – a có đồ thị (C’) là tịnh tiến (C) theo phương của Oy xuống dưới a đơn vị.
• Hàm số y = f(x + a) có đồ thị (C’) là tịnh tiến (C) theo phương của Ox qua trái a đơn vị.
• Hàm số y = f(x – a) có đồ thị (C’) là tịnh tiến (C) theo phương của Ox qua phải a đơn vị.
• Hàm số y = -f(x) có đồ thị (C’) là đối xứng của (C) qua trục Ox.
• Hàm số y = f(-x) có đồ thị (C’) là đối xứng của (C) qua trục Oy.
• Hàm số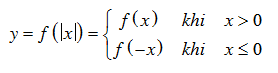 
có đồ thị (C’) bằng cách:
– Giữ nguyên phần đồ thị (C) nằm bên phải trục Oy và bỏ phần (C) nằm bên trái Oy.
– Lấy đối xứng phần đồ thị (C) nằm bên phải trục Oy qua Oy.
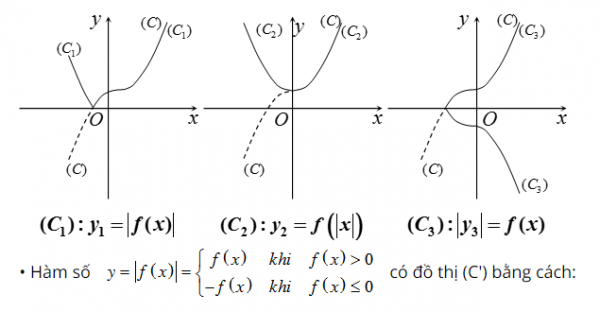
– Giữ nguyên phần đồ thị (C) nằm trên Ox.
– Lấy đối xứng phần đồ thị (C) nằm dưới Ox qua Ox và bỏ phần đồ thị (C) nằm dưới Ox.
Bài tập vận dụng :
Bài 1 :
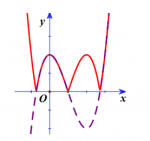
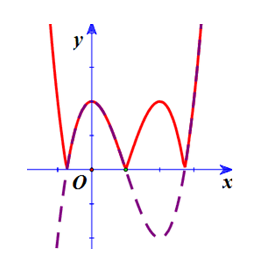
Vẽ đồ thị hàm số (C’): y = |x3 – 3×2 + 2| từ đồ thị (C): y = x3 – 3×2 + 2.
Giả sử (C) là đường đứt khúc trong hình vẽ.
Giải bài tập :
• Bước 1: Giữ nguyên đường đứt khúc phía trên trục Ox bằng cách tô đậm phần đường đứt khúc phía trên Ox.
• Bước 2: lấy đối xứng qua Ox phần đường đứt khúc nằm dưới Ox qua Ox rồi xóa phần đường đứt khúc nằm dưới Ox, ta được đồ thị (C’).
Bài 2 :
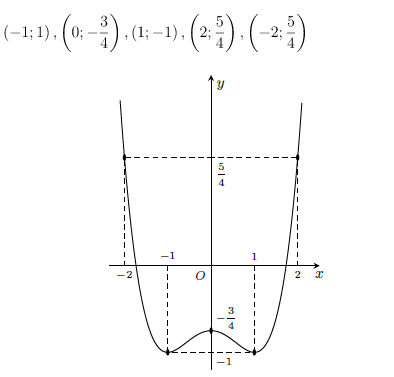
Khảo sát sự biến thiên và vẽ đồ thị của hàm số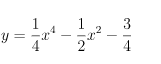 
Giải bài tập:
Tập xác định: D = ℝ
y’ = x3 − x;
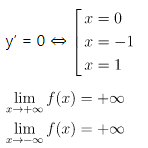
Từ bảng biến thiên:
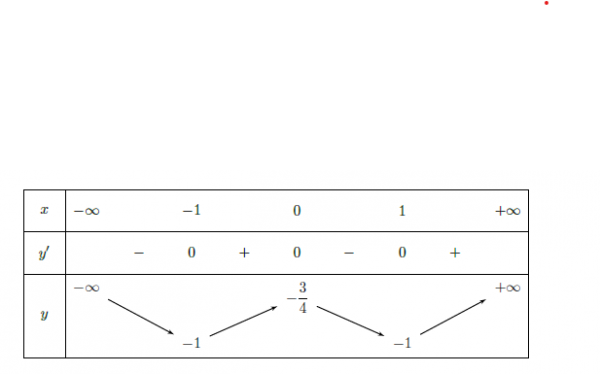
Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞), nghịch biến trên các khoảng (-∞; -1) và (0; 1).
Hàm số đạt cực đại tại x = 0 và yCĐ = , đạt cực tiểu tại x = ±1 và yCT = -1.
Đồ thị hàm số đi qua các điểm 