Công thức giải nhanh cực trị hàm bậc 3 của hàm sốluôn có trong các bài toán từ cơ bản đến nâng cao có trong các dạng bài tập cũng như các dạng đề thi khác nhau. Bierelarue sẽ giúp các bạn tìm hiểu nội dung cực trị hàm số bậc 3 là gì? Công thức tính nhanh cực trị hàm bậc 3? Lý thuyết và Bài tập về cực trị của hàm số bậc 3…để vận dụng vào làm bài tập một cách chuẩn xác nhất.
Xem các bài liên quan về cực trị của hàm số:
- Tìm cực trị của hàm số toán cao cấp và bài tập
- Cực trị hàm nhiều biến, Cực trị có điều kiện và không điều kiện
- Chuyên đề cực trị của hàm số lớp 12 và Bài tập vận dụng
Cực trị của hàm số là gì?
Cho hàm số y=f(x) liên tục và xác định trên khoảng (a;b) và điểm x0∈(a;b)
Hàm số f(x) đạt cực đại tại x0 nếu tồn tại số h>0 sao cho f(x)<f(x0) với mọi x∈(x0−h;x0+h) và x≠x0
Hàm số f(x) đạt cực tiểu tại x0 nếu tồn tại số h>0 sao cho f(x)>f(x0) với mọi x∈(x0−h;x0+h) và x≠x0
Định lý:
Cho hàm số y=f(x) liên tục, xác định và có đạo hàm cấp 2 trên khoảng (a;b). Khi đó
Nếu {f′(x0)=0f”(x0)>0⇒ x0 là điểm cực tiểu của hàm số f
Nếu {f′(x0)=0f”(x0)<0⇒ x0 là điểm cực đại của hàm số f
Cực trị của hàm số bậc 3 là gì?
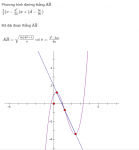
Cho hàm số bậc 3 y=f(x)=ax3+bx2+cx+d
Đạo hàm y′=f′(x)=3ax2+2bx+c
Hàm số f(x) có cực trị ⇔f(x) có cực đại và cực tiểu
⇔f′(x)=0 có hai nghiệm phân biệt ⇔Δ‘=b2−3ac>0
Hàm số f(x) không có cực trị ⇔Δ‘=b2−3ac≤0
- Tìm m để hàm số có 2 cực trị và bài tập vận dụng
- Số điểm cực trị của hàm số, Cực trị hàm tuyệt đối và bài tập.
Công thức tính nhanh cực trị hàm bậc 3
Đây là một số công thức giúp chúng ta có thể giải quyết các bài toán trắc nghiệm một cách nhanh chóng mà không cần phải tính toán phức tạp.
Cho hàm số y=ax3+bx2+cx+d có hai điểm cực trị phân biệt là A,B . Khi đó:
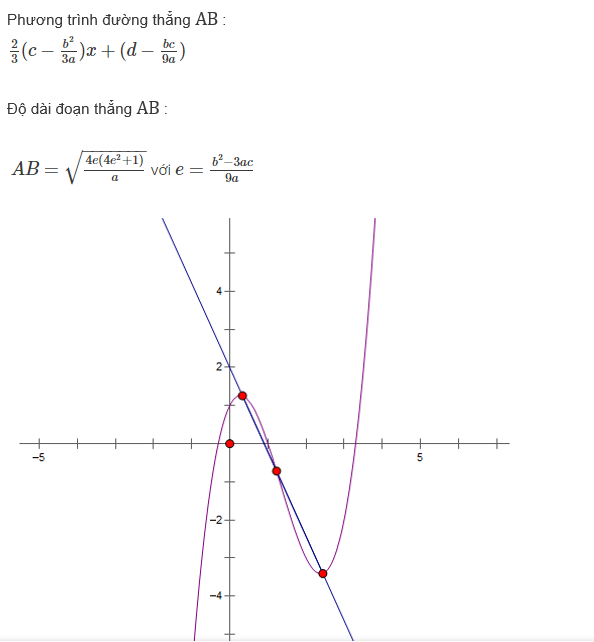
“
Bài tập về cực trị hàm đa thức bậc 3
Dạng 1: Tìm m để hai cực trị thỏa mãn điều kiện
Bài toán: Tìm m để hàm số y=f(x;m)=ax3+bx2+cx+d có 2 điểm cực trị x1;x2 thỏa mãn điều kiện K với a,b,c,d là các hệ chứa m
Cách làm:
Bước 1: Tập xác định D=R. Tính đạo hàm y′= 3ax2+2bx+c
Bước 2: Hàm số có 2 cực trị ⇔Δ‘=b2−3ac>0. Giải bất phương trình này tìm được m∈D1
Bước 3: Gọi x1;x2 là hai nghiệm của phương trình y′=0. Theo Vi-ét ta có :
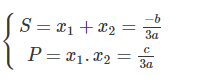
Bước 4: Biến đổi điều kiện yêu cầu của đề bài về dạng S và P. Từ đó giải ra tìm được m∈D2
Bước 5: Kết luận các giá trị của m thỏa mãn m=D1∩D2
Dạng 2: Tìm điểm cực trị hàm số bậc 3
Đây là dạng bài cơ bản nhất, chỉ cần sử dụng Định lý ở mục trên là có thể tìm được cực đại, cực tiểu của hàm số.
Ví dụ:
Tìm cực trị của hàm số : f(x)=x3−3×2−2
Cách giải:
Tập xác định D=R
Ta có :
f′(x)=3×2−6x=3x(x−2)
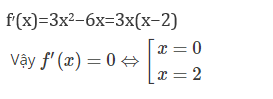
Mặt khác :
f′′(x)=6x−6
⇒f′′(0)=−6<0⇒ hàm số đạt cực đại tại điểm (0;−2)
f′′(2)=6>0⇒ hàm số đạt cực đại tại điểm (2;−6)
Dạng 3: Tìm m để hàm số bậc 3 có 2 cực trị
Bài toán: Tìm m để hàm số y=f(x;m)=ax3+bx2+cx+d có 2 điểm cực trị với a,b,c,d là các hệ chứa m
Cách làm:
Bước 1: Tập xác định D=R. Tính đạo hàm y′=3ax2+2bx+c
Bước 2: Hàm số có 2 cực trị ⇔Δ‘=b2−3ac>0
Bước 3: Giải bất phương trình trên, tìm ra điều kiện của m
- Sự đồng biến nghịch biến của hàm số – Toán 12 bài 1.
- Cực trị hàm nhiều biến, Cực trị có điều kiện và không điều kiện
Bài tập vận dụng :
Ví dụ 1 : Cho hàm số y = -x3 + 3×2 + 3(m2 – 1)x – 3m2 – 1 (m là tham số thực). Tìm m để hàm số có cực đại, cực tiểu và các điểm cực đại, cực tiểu này cách đều gốc tọa độ O.
Lời giải
Ta có đạo hàm y’ = – 3×2 + 6x + 3(m2 – 1),
y’ = 0 ⇔ – 3×2 +6x + 3(m2 – 1) = 0 (1)
Để hàm số có cực trị ⇔ y’ = 0 có 2 nghiệm phân biệt
⇔Δ’= m2 > 0 ⇔ m ≠ 0
Khi đó ta có tọa độ hai điểm cực trị là A(1 – m, – 2 – m2) và B(1+m ; -2 + 2m2)
Theo giả thiết đề bài 2 điểm cực trị này cách đều gốc tọa độ ta có
⇔ OA = OB
⇔ (1 – m)2+ (-2 – 2m2)2 = (1+ m)2 + (2 – 2m2)2
⇔4m3 = m
⇔ m = ± ½
Vậy với m = ± ½ thì hàm số có cực đại và cực tiểu thỏa mãn hai điểm này cách đều gốc tọa độ O.
Bài 2: cho hàm số y = x3 – 2(m + 1)x2 + (m2 – 3m + 2)x + 4. Tìm m để hàm số có cực đại, cực tiểu và 2 cực trị này nằm về hai phía của trục tung.
Lời giải
Tập xác định R
Ta có y’ = 3×2 – 2(m + 1)x + (m2 – 3m + 2)
Để hàm số có điểm cực đại, cực tiểu nằm về hai phía của trục tung thì phương trình y’ = 0 phải có 1 nghiệm phân biệt