Cực trị của hàm số là gì? Quy tắc tìm số điểm và bài tập cực trị của hàm số ra sao? Phương pháp giả bài tập Cực trị chứa hàm tuyệt đối. Cực trị có 2 quy tắc tìm số điểm cực trị của hàm số, dưới đây sẽ giới thiệu cho bạn đọc cách làm tìm cực trị của hàm số theo từng quy tắc một cách đầy đủ, chi tiết giúp các bạn đọc cũng như các em học sinh nắm rõ được để giải bài toán một cách chính xác nhất sau mỗi ví dụ minh họa.
Lý thuyết cực trị hàm số
Cực trị của hàm số là điểm có giá trị lớn nhất so với xung quanh và giá trị nhỏ nhất so với xung quanh mà hàm số có thể đạt được. Trong hình học, nó biểu diễn khoảng cách lớn nhất từ điểm này sang điểm kia và khoảng cách nhỏ nhất từ điểm này sang điểm nọ. Đây là khái niệm cơ bản về cực trị của hàm số.
Định nghĩa
Giả sử hàm số f xác định trên K (K ⊂ ℝ) và x0 ∈ K
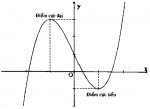
a) x0 được gọi là điểm cực đại của hàm số f nếu tồn tại một khoảng (a;b) ⊂ K chứa điểm x0 sao cho f(x) < f(x0), ∀ x ∈ (a;b) \{x0}
Khi đó f(x0) được gọi là giá trị cực đại của hàm số f.
b) x0 được gọi là điểm cực tiểu của hàm số f nếu tồn tại một khoảng (a;b) ⊂ K chứa điểm x0 sao cho f(x) > f(x0), ∀ x ∈ (a;b) \{x0}
→ Khi đó f(x0) được gọi là giá trị cực tiểu của hàm số f.
Chú ý:
1) Điểm cực đại (cực tiểu) x0 được gọi chung là điểm cực trị. Giá trị cực đại (cực tiểu) f(x0) của hàm số được gọi chung là cực trị. Hàm số có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập hợp K.
2) Nói chung, giá trị cực đại (cực tiểu) f(x0) không phải là giá trị lớn nhất (nhỏ nhất) của hàm số f trên tập K; f(x0) chỉ là giá trị lớn nhất (nhỏ nhất) của hàm số f trên một khoảng (a;b) chứa x0.
- Số chẵn số lẻ là gì? Số chẵn là những số nào, số lẻ là những số nào?
- Số lớn nhất có 1,2,3,4,5 chữ số chẵn lẻ khác nhau là chữ số nào?
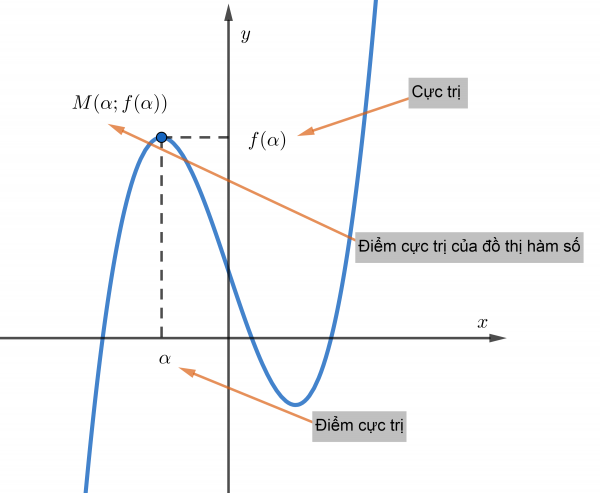
3) Nếu x0 là một điểm cực trị của hàm số f thì điểm (x0; f(x0)) được gọi là điểm cực trị của đồ thị hàm số f.
Quy tắc tìm các điểm cực trị của hàm số:

Bài tập cực trị của hàm số :




Phương pháp tìm cực trị của hàm tuyệt đối :

Bài tập ứng dụng :
Bài 1 : Cho hàm số y = f ( x ) có bảng biến thiên như hình vẽ dưới :
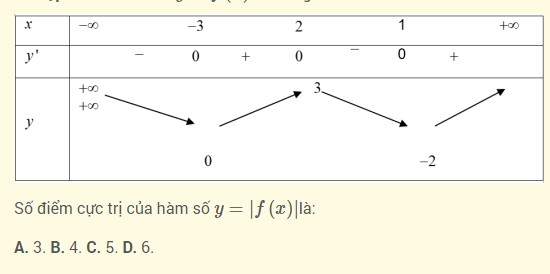
Lời giải :

Bài 2 : Cho hàm số y = f ( x ) có bảng biến thiên như hình vẽ dưới :
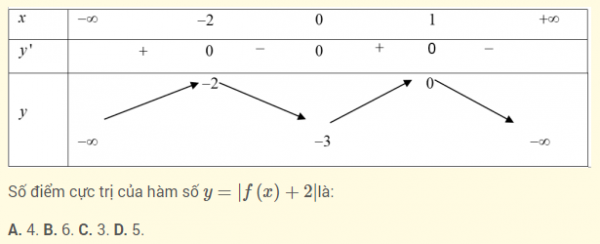
Lời giải :

Xem thêm tại đây :
Tìm cực trị của hàm số, Giá trị cực đại của hàm số
Sự đồng biến nghịch biến của hàm số – Toán 12 bài 1.
Trọng tâm tam giác vuông, cân: Tính chất, Công thức và Cách tính tọa độ.
Bảng đơn vị đo diện tích – Đổi đơn vị đo diện tích mét vuông lớp 4.