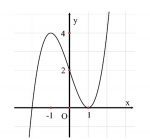
Tìm m để hàm số có 2 cực trị đây là một dạng toán về cực trị của hàm số đa thức bậc 3 y= ax3 + bx2 + cx + d ( a #0 ). Chúng tôi sẽ tóm tắt nội dung và bài tập để giúp các bạn có thêm kiến thức bổ ích giải các bài toán chuẩn xác, Những bài toán nằm trong câu hỏi phụ của khảo sát hàm số hết sức đa dạng và trong đó cực trị hàm số bậc 3 là một dạng toán phổ biến nhất.
Tìm m để hàm số đa thức bậc 3 có 2 cực trị:
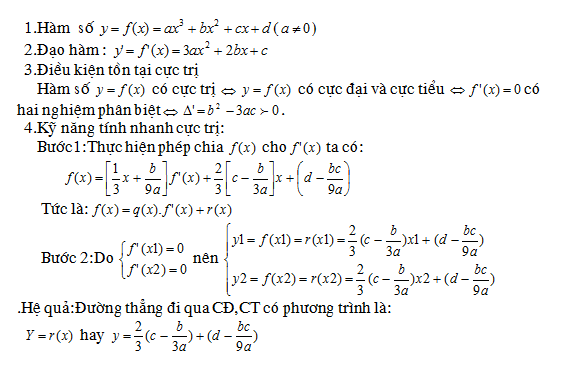

- Bảng đơn vị đo diện tích – Đổi đơn vị đo diện tích mét vuông lớp 4.
- Số chẵn số lẻ là gì? Số chẵn là những số nào, số lẻ là những số nào?
- Số lớn nhất có 1,2,3,4,5 chữ số chẵn lẻ khác nhau là chữ số nào?
Tìm m để hàm số đa thức bậc 3 có 2 cực trị trái dấu :

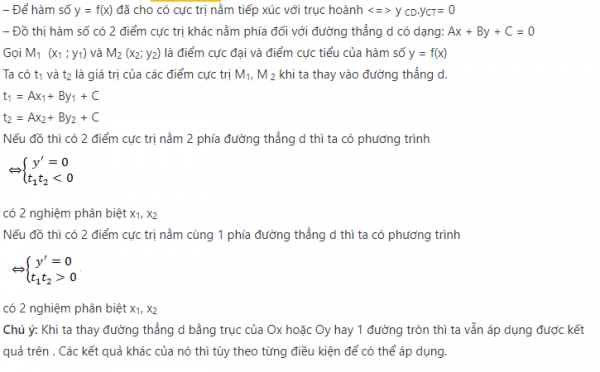
ví dụ :

Tìm m để hàm số đa thức bậc 3 có 2 điểm cực trị trái dấu :

Bài tập vận dụng :
Bài 1: Với giá trị nào của m thì hàm số y = x3 – 3×2 + 3(1 – m2)x + 1 có 2 điểm cực trị.
A. m ≠ 1
B. m ∈ R
C. m ≠ 0
D. Không tồn tại m
Lời giải
Chọn C
Ta có y’ = 3×2-6x + 3(1 – m2); y’ = 0 ⇔ x2-2x + 1 – m2 = 0
Hàm số đã cho có 2 điểm cực trị ⇔ phương trình y’ = 0 có hai nghiệm phân biệt
⇔ Δ’ > 0 ⇔ 1 – (1 – m2)>0 ⇔ m2>0 ⇔ m ≠ 0
Bài 2 : Với giá trị nào của m thì hàm số H10 có cực trị?

Bài 3 :Cho hàm số y = -2×3 + (2m – 1)x2 – (m2 – 1)x – 2. Số giá trị nguyên của m để hàm số đã cho có hai điểm cực trị là:
A. 3
B. 5
C. 6
D. 8
Lời giải
Chọn B
Ta có y’ = -6×2 + 2(2m – 1)x – (m2 – 1)
Hàm số đã cho có 2 điểm cực trị ⇔ phương trình y’ = 0 có hai nghiệm phân biệt
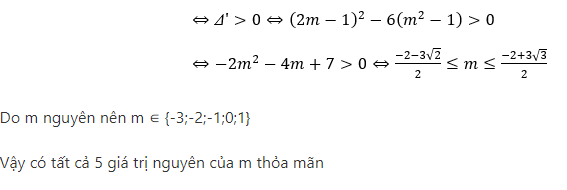
Xem thêm tại đây :
Số điểm cực trị của hàm số, Cực trị hàm tuyệt đối và bài tập.
Tìm cực trị của hàm số, Giá trị cực đại của hàm số
Sự đồng biến nghịch biến của hàm số – Toán 12 bài 1.
Trọng tâm tam giác vuông, cân: Tính chất, Công thức và Cách tính tọa độ.