Ở bài 1 chúng ta đã đi tìm hiểu xem thế nào là sự đồng biến và nghịch biến của hàm số, bài này chúng ta cùng nhau đi tìm hiểu Giá trị cực đại của hàm số và cách tìm cực trị của hàm số. Sau khi các em đã quen với các bài toán xét tính đơn điệu của hàm số thì bước tiếp theo các em cần nắm vững được kiến thức để giải bài tập về cực trị của hàm số đây là dạng toán thường xuyên có trong các đề thi tốt nghiệp THPT. Vậy chúng ta cùng nhau ôn lại kiến thức ở bài này nhé.
Khái niệm về cực đại cực tiểu của hàm số :
Định nghĩa cực trị :

Điều kiện đủ để hàm số có cực trị:

Quy tắc tìm cực trị của hàm số :
Chú ý.
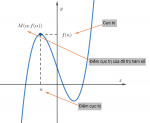
Nếu hàm sốy=f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCÑ (fCT), còn điểm M(x0;f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
Tính chất và dấu hiệu nhận biết hình thang cân, vuông.
Số lớn nhất có 1,2,3,4,5 chữ số chẵn lẻ khác nhau là chữ số nào?
Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
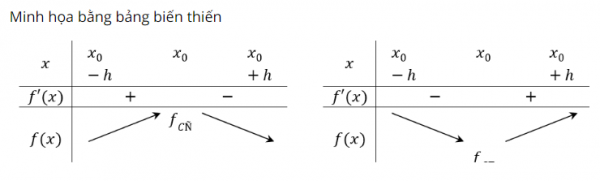
Quy tắc tìm cực trị của hàm số
Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x). Giải phương trình f'(x)và ký hiệuxi (i=1,2,3,…)là các nghiệm của nó.
Bước 3. Tính f”(x) và f”(xi ) .
Bước 4. Dựa vào dấu của f”(xi )suy ra tính chất cực trị của điểm xi.
Phương pháp tìm cực đại và cực tiểu
Từ đó, có các bước xác định cực trị như sau:
Bước 1: Tính đạo hàm f′(x), tìm những điểm mà tại đó f′(x)= 0 hoặc f′(x) không xác định.
Bước 2:
Cách 1: Xét dấu f’(x) dựa vào định lí 2 để kết luận điểm cực đại, cực tiểu. Nếu f’(x) đổi dấu khi x quá xo thì hàm số có cực trị tại xo.
Cách 2: Xét dấu f′′(xo) với xo là nghiệm của f’(x) dựa vào định lí 3 để kết luận.
Nếu f”(xo) < 0 thì hàm số đạt cực đại tại điểm xo.
Nếu f”(xo) > 0 thì hàm số đạt cực tiểu tại điểm xo.
Chú ý: Hàm số phân thức bậc nhất trên bậc nhất
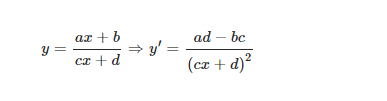
Dấu của đạo hàm không phụ thuộc vào x, hay độc lập với x nên hàm số luôn đồng biến hoặc luôn nghịch biến trên các khoảng xác định của nó. Do đó hàm số luôn không có cực trị.
Bài tập vận dụng :
Bài 1 : Tìm cực trị của hàm số y = -x3 + 3×3 – 3x + 2
lời giải :
Tập xác định D = R.
Tính y’ = -3×2 + 6x-3.
Cho y’= 0 ⇔ -3×2+ 6x-3 = 0 ⇔ x = 1.
Bảng biến thiên
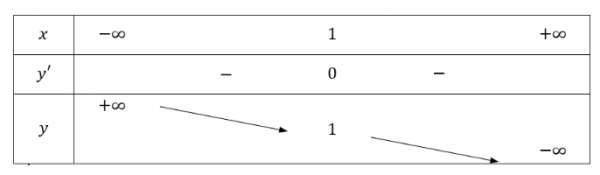
Vậy hàm số đã cho không có cực trị.
Bài 2 : Tìm cực trị của hàm số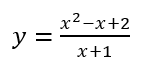
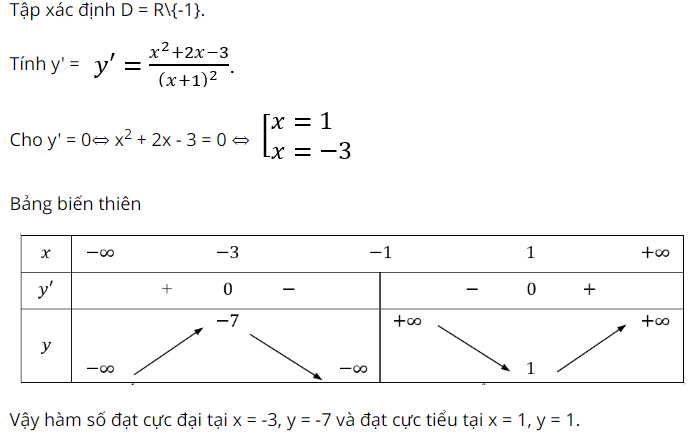
lời giải:
xem thêm tại đây:
Sự đồng biến nghịch biến của hàm số – Toán 12 bài 1.
Trọng tâm tam giác vuông, cân: Tính chất, Công thức và Cách tính tọa độ.
Bảng đơn vị đo diện tích – Đổi đơn vị đo diện tích mét vuông lớp 4.
Số chẵn số lẻ là gì? Số chẵn là những số nào, số lẻ là những số nào?