Toán học là môn chủ đạo để các em hoàn thành tư duy logic của mình, với những dạng bài toán khác nhau nên tư duy logic cũng khác nhau. Bài này chúng ta sẽ cùng nhau đi tìm hiểu về Định nghĩa, Đạo hàm, Tính chất của hàm số lũy thừa trong toán học 12, Mong rằng giúp các em học sinh có nhiều kiến thức bổ ích hơn nữa trong việc giải bài tập.
Hàm số lũy thừa:
Định nghĩa: Hàm số y = xα với α ∈ R được gọi là hàm số lũy thừa.
Tập xác định: Tập xác định của hàm số y = xα là:
• D = R nếu α là số nguyên dương.
• D = R \ {0} với α nguyên âm hoặc bằng 0
• D = (0; +∝) với α không nguyên.
Đạo hàm: Hàm số y = xα có đạo hàm với mọi x > 0 và (xα)’ = α.xα – 1.
Chú ý :
- Hàm số lũy thừa là gì? Đạo hàm với số mũ tổng quát và khảo sát hàm số lũy thừa
- Lũy thừa của một số hữu tỉ : Công thức và bài tập Toán lớp 7
Tính chất của hàm số lũy thừa trên khoảng (0; +∝).
- y = xα, α > 0 :
a. Tập khảo sát: (0; +∝)
b. Sự biến thiên
+ y’ = αxα – 1 > 0, ∀x > 0
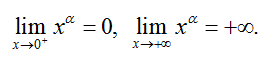
+ Giới hạn đặc biệt
+ Tiệm cận: không có
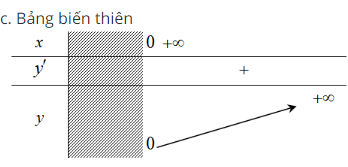
- y = xα, α < 0
a. Tập khảo sát: (0; +∝)
b. Sự biến thiên
+ y’ = αxα – 1 < 0, ∀x > 0
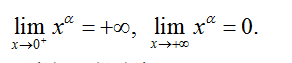
+ Giới hạn đặc biệt
+ Tiệm cận: không có
– Trục 0x là tiệm cận ngang
– Trục 0y là tiệm cận đứng.

Đồ thị lũy thừa của hàm số

Đồ thị của hàm số lũy thừa y = xα luôn đi qua điểm I(1; 1)
Lưu ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó. Chẳng hạn: y = x3, y = x-2, y = xπ
Xem thêm tại đây :
- Khảo sát và vẽ đồ thị hàm số toán học 12
- Định nghĩa tiệm cận ngang, Công thức tính tiệm cận ngang là gì?
Bài tập vận dụng :
Bài 1 :
Tìm tập xác định của các hàm số:
![]()
Phương pháp giải:
Tập xác định của hàm số lũy thừa y=xn tùy thuộc vào giá trị của n:
Với n là số nguyên dương, tập xác định là R.
Với n là số nguyên âm hoặc bằng 0, tập xác định là R∖{0}.
Với n không nguyên, tập xác định là (0;+∞)
Lời giải:
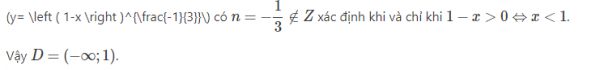
Bài 2 :
y=(x2−1)−2;
Phương pháp giải:
Tập xác định của hàm số lũy thừa y=xn tùy thuộc vào giá trị của n:
Với n là số nguyên dương, tập xác định là R.
Với n là số nguyên âm hoặc bằng 0, tập xác định là R∖{0}.
Với n không nguyên, tập xác định là (0;+∞)
Lời giải chi tiết:
y=(x2−1)−2 có n=−2∈Z− xác định khi và chỉ khi x2−1≠0⇔x≠±1.
Vậy D=R∖{−1;1} .

