Tổng hợp 2 dao động điều hòa , Phương pháp giản đồ FRE-NEN

Tổng hợp 2 dao động điều hòa cùng phương cùng tần số, Phương pháp giản đồ FRE-NEN là chuyên đề quan trọng trong việc ôn tập lại kiến thức để giải bài tập trên máy tính cũng như bằng phương pháp đơn giản để chuẩn bị cho các kì thi THPT quốc gia khác nhau, Hai phương pháp giải bài tập tổng hợp dao động điều hòa. Hi vọng giúp các em hiểu rõ những kiến thức trọng tâm và phương pháp giải bài tập.

Phương pháp giản đồ FRE-NEN

Vectơ quay
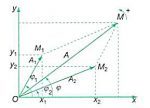
Khi điểm M chuyển động tròn đều thì vectơ vị trí \overline{OM}
OM
quay đều với cùng tốc độ góc w. Khi ấy x = Acos(wt + j) là phương trình hình chiếu của vectơ quay \overline{OM}
OM
trên trục x.
Biểu diễn phương trình của dao động điều hòa bằng một vectơ quay được vẽ tại thời điểm ban đầu như hình vẽ. Vectơ quay có những đặc điểm sau đây
Có gốc taị gốc tọa độ của trục Ox;
Có độ dài bằng biên độ dao động, OM = A;
Hợp với trục Ox một góc bằng pha ban đầu (chọn chiều dương là chiều của đường tròn lượng giác).

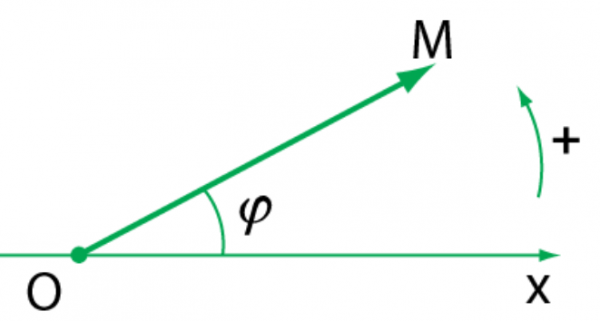
Phương pháp giản đồ Fre-nen: Lần lượt vẽ hai vec tơ quay biểu diễn hai phương trình dao động thành phần. Vectơ tổng của hai vectơ thành phàn biểu diễn phương trình của dao động tổng hợp (Hình 5.1).

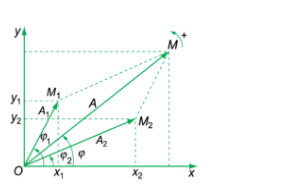
Nếu một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số với các phương trình:

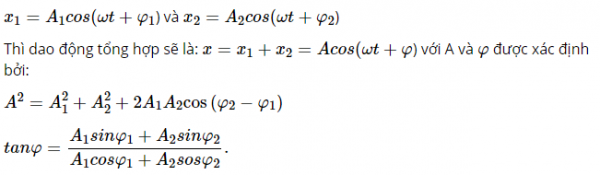
Ảnh hưởng của độ lệch pha
Biên độ của dao động tổng hợp phụ thuộc vào các biên độ A1, A2 và độ lệch pha (φ2 – φ1) của các dao động thành phần.

Nếu các dao động thành phần cùng pha, tức ∆φ = φ2 – φ1 = 2nπ, (n = 0, ± 1, ± 2,…), thì biên độ dao động tổng hợp là lớn nhất và bằng tổng hai biên độ: A = A1 + A2.
Nếu hai dao động thành phần ngược pha, tức ∆φ = φ2 – φ1 = (2n + 1)π, (n = 0, ± 1, ± 2,…), thì biên độ dao động tổng hợp là nhỏ nhất: A = |A1 – A2|.

Chuyên đề dao động điều hòa vật lý 12

Tổng hợp dao động điều hòa, Trong dao động điều hòa gia tốc biến đổi? và bài tập

Điện năng công suất điện là gì ? Công suất tỏa nhiệt

Tổng hợp 2 dao động điều hòa cùng phương cùng tần số

Tổng hợp nhiều dao động
Đề bài: Một vật thực hiện đồng thời n dao động thành phần với:

x1 = A1cos(ωt + φ1)
x2 = A2cos(ωt + φ2)

xn = Ancos(ωt + φn)
Tìm dao động tổng hợp
Phương trình dao động tổng hợp có dạng: x = Acos(ωt + φ)

Vi dụ minh họa:

Bài toán: Giả sử một vật thực hiện đồng thời 2 dao động x1 = A1cos(ωt + φ1) và x2 = A2cos(ωt + φ2). Xác định phương trình dao động tổng hợp của chúng.

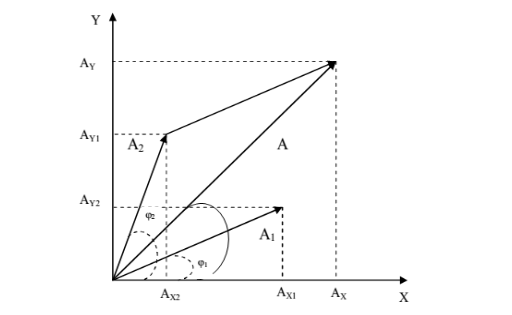
Tìm phương trình dao động thành phần

Bài toán: Một vật thực hiện đồng thời 2 dao động điều hòa x1, x2. Ta biết x1 = A1cos(ωt + φ1) và dao độngtổng hợp của chúng là: x = Acos(ωt + φ). Tìm dao động x2.

Bài làm: Phương trình dao động thành phần x2 có dạng: x2 = A2cos(ωt + φ2)

Bài tập vận dụng:

Bài tập 2: Một vật thực hiện hai dao động điều hòa với phương trình lần lượt là x1 = 4cos(6πt + π/3); x2 = cos(6πt + π) cm. Hãy xác định vận tốc cực đại mà dao động có thể đạt được.

A. 54π cm/s B. 6π cm/s C. 45cm/s D. 9π cm/s

Trả lời

Ta có: Vmax = A.ω ⇒ Vmax khi Amax Với Amax = 9 cm khi hai dao động cùng pha

⇒ Vmax = 9.6π = 54π cm/s.

Bài 3 :

Nêu ảnh hưởng của độ lệch pha (φ2 – φ1) đến biên độ của dao động tổng hợp trong các trường hợp:

a) Hai dao động thành phần cùng pha

b) Hai dao động thành phần ngược pha

c) Hai dao động thành phần có pha vuông góc

Lời giải:

Biên độ của dao động tổng hợp phụ thuộc vào các biên độ A1, A2 và độ lệch pha (φ2 – φ1) của các dao động thành phần.

a) Nếu các dao động thành phần cùng pha, tức ∆φ = φ2 – φ1 = 2nπ, (n = 0, ± 1, ± 2,…), thì biên độ dao động tổng hợp là lớn nhất và bằng tổng hai biên độ: A = A1 + A2.

b) Nếu hai dao động thành phần ngược pha, tức ∆φ = φ2 – φ1 = (2n + 1)π, (n = 0, ± 1, ± 2,…), thì biên độ dao động tổng hợp là nhỏ nhất: A = |A1 – A2|.

c) Nếu hai dao động thành phần vuông pha