Trong toán hình bình hành ngoài công thức tính diện tích và chu vi hình bình hành thì lý thuyết về hình bình hành cũng đặc biệt quan trọng , nó chiếm 1/3 trong bài tập về nhà . Chính vì vậy nắm vững tính chất hình bình hành , dấu hiệu nhận biết hình bình hành là cực kỳ cần thiết . Bài học ngày hôm nay chúng ta sẽ cùng ôn tập về lý thuyết hình bình hành là gì nhé !
Hình bình hành là gì ?
Hình bình hành là một hình tứ giác được tạo thành khi hai cặp đường thẳng song song cắt nhau. Nó là một dạng đặc biệt của hình thang. hình bình hành là tứ giác có các cạnh đối song song.
Chứng minh tứ giác ABCD là 1 hình bình hành như sau :
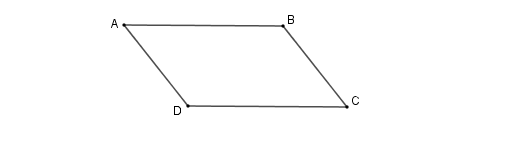
Tứ giác ABCD là một hình bình hành khi và chỉ khi : AB // CD , AD // BC .
Tính chất hình bình hành .
Các cạnh đối song song và bằng nhau.
Các góc đối bằng nhau.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Dấu hiệu nhận biết hình bình hành .
Hình bình hành là một tứ giác đặc biệt
Tứ giác có hai cặp cạnh đối song song là hình bình hành.
Tứ giác có các cạnh đối bằng nhau là hình bình hành.
Tứ giác có hai cạnh đối vừa song song và vừa bằng nhau là hình bình hành.
Tứ giác có các góc đối bằng nhau là hình bình hành.
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Hình bình hành là hình thang
Hình thang có hai cạnh đáy bằng nhau là hình bình hành.
Hình thang có hai cạnh bên song song là hình bình hành
Bài tập về tính chất và dấu hiệu nhận biết của hình bình hành .
Bài tập 1
Phát biểu nào dưới đây về hình bình hành là sai
1. Tứ giác có các cạnh đối song song là hình bình hành.
2. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
3. Tứ giác có hai góc đối bằng nhau là hình bình hành.
4. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình
Đáp án : 3
Chứng minh như sau :
Như trên ta có dấu hiệu nhận biết hình bình hành như sau :
Tứ giác có các cạnh đối song song là hình bình hành.
Tứ giác có các cạnh đối bằng nhau là hình bình hành.
Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Tứ giác có các góc đối bằng nhau là hình bình hành.
Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Chọn đáp án sai là 3
Bài tập 2 :
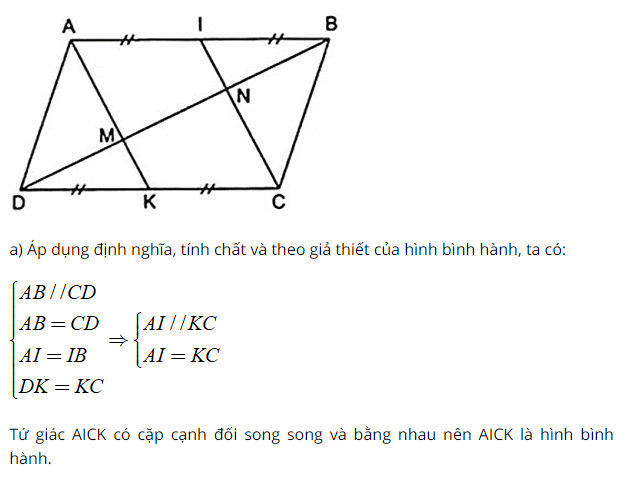
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh :
a) AK//CI
b) DM = MN = NB
Lời giải