Bạn đang tìm hiểu về công thức tính diện tích tam giác ở toán học lớp 5 , Bài viết hôm nay chúng tôi sẽ cung cấp cho các bạn đầy đủ công thức tính tam giác vuông , tam giác thường , tam giác đều và tam giác cân . Các công thức này nên cho các con học thuộc lòng để áp dụng vào các bài thi ở trường .
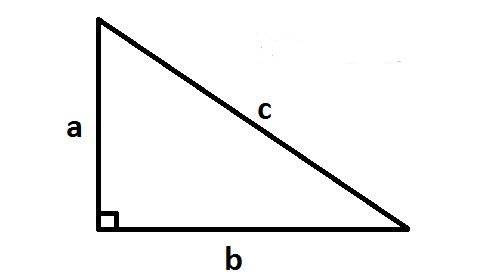
Định nghĩa tam giác vuông, cân , thường , đều .
Định nghĩa Tam giác vuông là một tam giác có một góc là góc vuông 90 độ .
Định nghĩa Tam giác cân là tam giác có hai cạnh bằng nhau.
Định nghĩa tam giác đều là tam giác có ba cạnh bằng nhau bằng 60°
Định nghĩa tam giác thường là tam giác có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau. Tam giác thường cũng có thể bao gồm các trường hợp đặc biệt của tam giác
Công thức tính diện tích tam giác .
Công thức tính tam giác Vuông
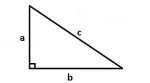
Tam giác như hình vẽ có cạnh góc vuông tại B : a và b được gọi là độ dài cạnh góc vuông .
Theo công thức tính diện tích tam giác vuông sẽ như sau :
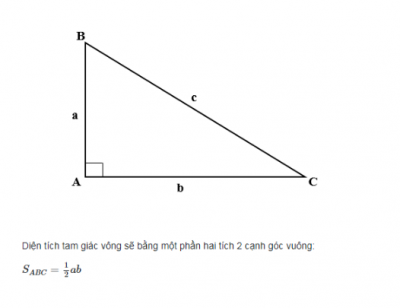Công thức như sau : Diện tích tam giác vuông sẽ bằng một phần hai cạnh góc vuông
Kí hiệu :
S : diện tích tam giác vuông
ab : độ dài cạnh góc vuông
Cách tính diện tích tam giác thường
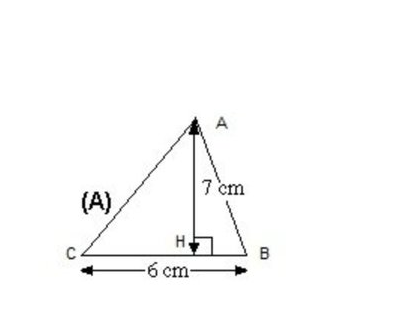
Diện tích tam giác thường tính bằng cách nhân chiều cao với độ dài đáy, lấy kết quả đó chia cho 2. Diện tích tam giác thường bằng 1/2 tích của chiều cao và chiều dài cạnh đáy tam giác.
Công thức tính diện tích tam giác thường :S = (a x h)/ 2
Kí hiệu
a: Chiều dài đáy tam giác
h: Chiều cao tam giác
Từ công thức trên suy ra: h= (sx2)/a hoặc a= (sx2)/h.
Tính diện tích tam giác khi biết một góc
Diện tích tam giác bằng ½ tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.
Tính diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R).
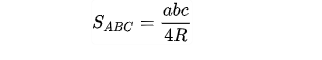
Công thức tính diện tích tam giác vuông cân .
Tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông:
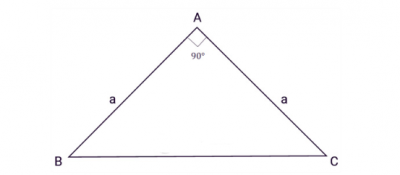
Từ công thức tính diện tích tam giác vuông cho diện tích tam giác vuông cân với chiều cao và cạnh đáy bằng nhau, ta có công thức:
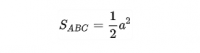
Công thức tính diện tích tam giác đều .
Tam giác đều ABC có ba cạnh bằng nhau, a là độ dài các cạnh như hình dưới đây
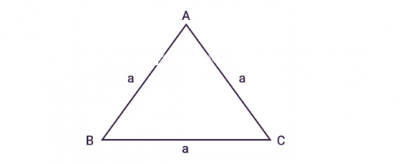
Áp dụng định lý Heron ta có thể suy ra như sau, ta có công thức tính diện tích tam giác đều:
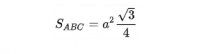
Tính diện tích tam giác cân
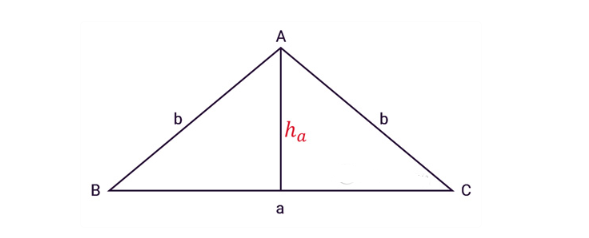
Như hình vẽ sau ta có tam giác cân ABC có ba cạnh
kí hiệu như sau :
a : là độ dài cạnh đáy,
b : là độ dài hai cạnh bên,
ha : là đường cao từ đỉnh A
Áp dụng công thức tính diện tích thường, ta có công thức tính diện tích tam giác cân:
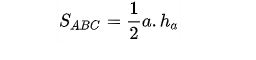
Trên đây là toàn bộ công thức tính tam giác vuông cân dần đều cho học sinh lớp 5 nhanh nhất . Phụ hung nên cho học sinh nhớ rõ những công thức tam giác này để áp dụng vào các bài tập thực tế .
Bài tập ví dụ.
Ví dụ 1 : Cho tam giác ABC vuông cân tại A, có AB = AC = 8cm. Tính diện tích tam giác ABC.
Lời giải:
Do cạnh AB = AC = a = 8cm
Xét tam giác ABC vuông cân tại A, ta có:
S = (a2) : 2 = 64 : 2 = 32 cm²
Ví dụ 2 : Tính diện tích tam giác có chiều cao 18dm, chiều cạnh đáy bằng 130cm
Áp dụng công thức tính diện tích tam giác.
Lời giải:
Đổi 130cm = 13dm
Diện tích hình tam giác là: (18 x 13) : 2 = 117 cm2
Đáp số: 117cm2