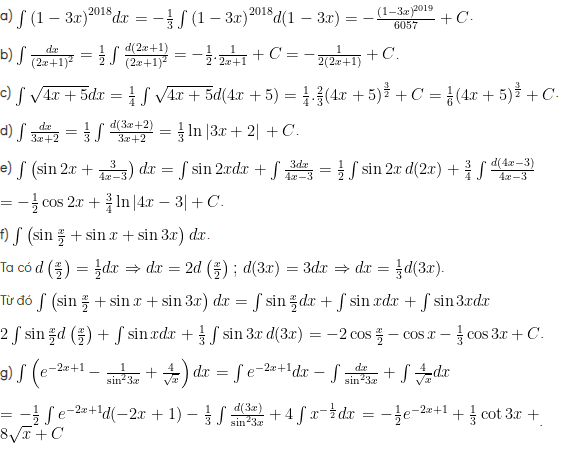Ở chương này chúng ta cùng nhau đi tìm hiểu xem Định nghĩa về nguyên hàm, Tính chất và phương pháp tính nguyên hàm. Bài toán nguyên hàm là không thể thiếu trong chương trình học chính thức trên nhà trường cũng như luyện thi đại học. Đây là lớp bài toán quan trọng, có liên quan mật thiết với nhau. Tính thành thạo đạo hàm của hàm số, có thể giúp chúng ta suy luận để hướng tới kết quả của bài toán tìm nguyên hàm, cũng như kiểm tra tính đúng đắn của kết quả. Ngược lại, tính thành thạo nguyên hàm, có thể giúp ta tính được nhiều tích phân đơn giản của các hàm số khác nhau… về sau.
NGUYÊN HÀM VÀ TÍNH CHẤT
1. Nguyên hàm
Định nghĩa: Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
Định lí:
1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x) + C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu ∫f(x)dx = F(x) + C
Xem thêm tại đây :
- Bất phương trình logarit là gì?, Phương pháp giải và Bài tập Bất phương trình logarit
- Phương trình lôgarit là gì? Các cách giải và bài tập phương trình lôgarit
- Phương trình mũ là gì? Bất phương trình và các phương pháp giải phương trình mũ
2. Tính chất của nguyên hàm
Tính chất 1: (∫f(x)dx)’ = f(x) và ∫f'(x)dx = f(x) + C
Tính chất 2: ∫kf(x)dx = k∫f(x)dx với k là hằng số khác 0.
Tính chất 3: ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx
3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
4. Bảng nguyên hàm của một số hàm số sơ cấp

PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
1. Phương pháp đổi biến số
Định lí 1: Nếu ∫f(u)du = F(u) + C và u = u(x) là hàm số có đạo hàm liên tục thì
∫f(u(x))u'(x)dx = F(u(x)) + C
Hệ quả: Nếu u = ax + b (a ≠ 0) thì ta có ∫f(ax + b)dx = (1/a)F(ax + b) + C
2. Phương pháp nguyên hàm từng phần
Định lí 2: Nếu hai hàm số u = u(x) và y = y(x) có đạo hàm liên tục trên K thì
∫u(x)v'(x)dx = u(x)v(x) – ∫u'(x)v(x)dx
Hay ∫udv = uv – ∫vdu
Bài tập vận dụng :
Bài 1 : Tìm một nguyên hàm F(x) của hàm số ![]()
Hướng dẫn giải
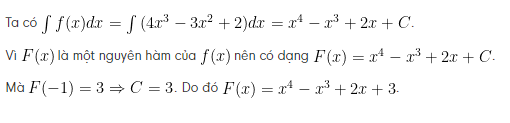
Bài 2 :
Gọi f(x) là một nguyên hàm của f(x) ![]()
Hướng dẫn giải
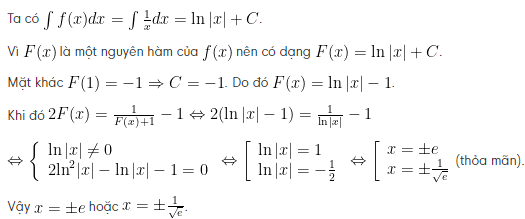
Bài 3 :
tìm các nguyên hàm của các hàm số sau:
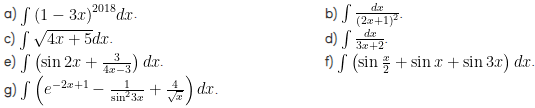
Hướng dẫn giải