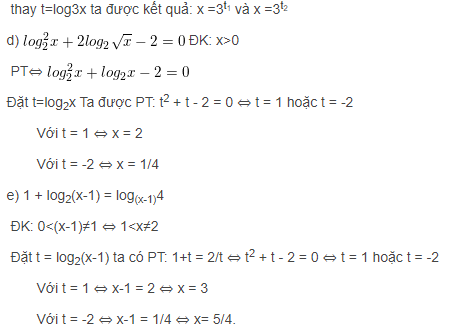Chúng ta đã cùng nhau đi tìm hiểu định nghĩa, công thức về phương trình logarit, trong bài này chúng ta cùng nhau đi tìm hiểu về Bất phương trình logarit là gì?, Phương pháp giải và Bài tập Bất phương trình logarit. Vì kiến thức này được nằm trong kiến thức toán học có trong đề thi THPT của các năm học nên các em cần nắm vững để giải bài tập, Xin mời các em cùng tìm hiểu.
Phương trình lôgarit là gì? Các cách giải và bài tập phương trình lôgarit
Phương trình mũ là gì? Bất phương trình và các phương pháp giải phương trình mũ
Bất phương trình logarit cơ bản :
+ Xét bất phương trình logax > b
Nếu a > 1 thì log ax > b <=> x > a^b
Nếu 0 < a < 1 thì log ax > b <=> 0 < x < a^b
Phương pháp giải phương trình và bất phương trình logarit :
Giải phương trình logarit, Bất phương trình logarit bằng phương pháp đưa về cùng cơ số :
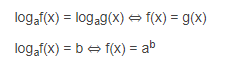
Lưu ý : Đối với các PT, BPT logarit ta cần đặt điều kiện để các biểu thức logaf(x) có nghĩa tức là f(x) > hoặc = 0
Ví dụ : Giải bất phương trình:
![]()
Bài làm :

Kết hợp với điều kiện, bất phương trình có tập nghiệm: S = [ – 1; 3)
Giải phương trình logarit, Bất phương trình logarit bằng phương pháp đặt ẩn phụ :
+ Với các PT, BPT logarit mà có thể biểu diễn theo biểu thức logaf(x) thì ta có thể sử dụng phép đặt ẩn phụ t = logaf(x).
+ Ngoài việc đặt điều kiện để có biểu thức logaf(x) có nghĩa f(x) > 0 thì chúng ta cần chú ý đến đặt điểm của PT, BPT logarit đang xét có chứa căn có ẩn ở mẫu hay không khi đó ta phải đặt điều kiện cho PT, BPT có nghĩa.
Ví dụ : Giải bất phương trình:
![]()
Bài làm :

Giải phương trình logarit, Bất phương trình logarit bằng phương pháp mũ hóa :
+ Đôi khi ta không thể giải PT, BPT logarit bằng cách đưa về cùng cơ số hay dùng ấn phụ được khi đó ta thể đặt x = a^t PT, BPT cơ bản ( phương pháp này gọi là mũ hóa )
Nhận biết phương trình : PT loại này thường chứa nhiều cơ số khác nhau.
Bài tập :
Bài 1 : Giải các phương trình sau :
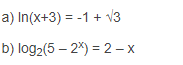
Hướng dẫn giải :

Bài 2 : Giải các phương trình sau :
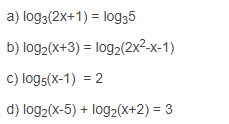
Hướng dẫn giải :
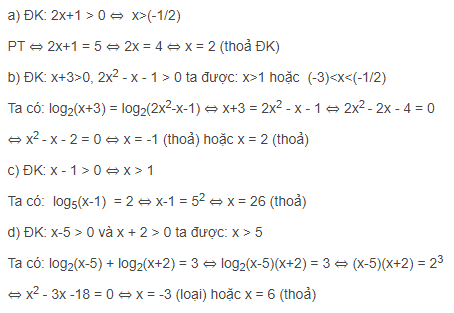
Bài 3 : Giải các phương trình sau :
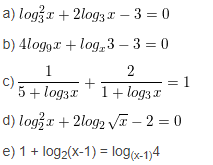
Hướng dẫn giải :