Trong toán học lớp 12, Nguyên hàm tích phân từng phần là một trong những nội dung quan trọng thường xuất hiện trong các đề thì tốt nghiệp THPT quốc gia. Để nắm rõ được kiến thức quan trọng nhất thì dưới đây chúng tôi sẽ tổng hợp lại các kiến thức quan trọng, Hi vọng sẽ giúp các em nắm được kiến thức để làm bài tập môn toán học để lấy điểm một cách tối đa nhất có thể.
Khái niệm về tích phân từng phần :
Trong vi tích phân nói riêng, và trong giải tích toán học nói chung, tích phân từng phần là quá trình tìm tích phân của tích các hàm dựa trên tích phân các đạo hàm và nguyên hàm của chúng. Nó thường được sử dụng để biến đổi nguyên hàm của tích các hàm thành một nguyên hàm mà đáp án có thể được tìm thấy dễ dàng hơn. Quy tắc có thể suy ra bằng cách tích hợp quy tắc nhân của đạo hàm.
– Nếu u(x) và v(x) là các hàm số có đạo hàm liên tục trên (a,b) thì :
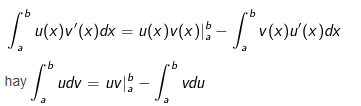
Định lý
Định lý có thể được suy ra như sau. Giả sử u(x) và v(x) là hai hàm khả vi liên tục. Quy tắc nhân phát biểu rằng
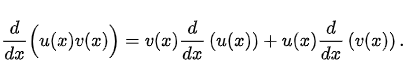
Tích phân cả hai vế đối với x, 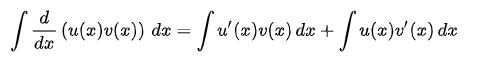
sau đó áp dụng định nghĩa của nguyên hàm, 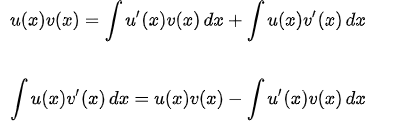
cho ta công thức tích phân từng phần.
Bởi vì du và dv là các vi phân của một hàm một biến x,
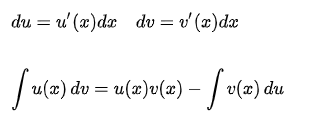
Tích phân gốc ∫uv′ dx chứa v′ (đạo hàm của v); để áp dụng định lý, phải tim nguyên hàm v (của v′), và tính tích phân ∫vu′ dx.
Áp dụng công thức ở trên ta có cách tính tích phân từng phần :
– Bước 1 : Viết f(x)dx dưới dạng udv = uv’dx bằng cách chọn một phần tích hợp của f(x) làm u(x) và phần còn lại dv=v'(x)dx.
– Bước 2 :Tính du = u’dx và v = ![]()
– Bươc 3 : Tính 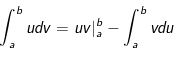
Một số dạng bài tập tính tích phân từng phần.
– Tính tích phân hàm đa thức P(x) và hàm lượng giác (sinx, cosx) 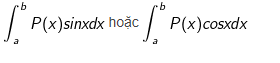
+ Ta đặt u = P(x), dv = sinxdx hoặc (dv = cosxdx)
– Tính tích phân hàm đa thức P(x) và hàm logarit nepe (inx) : 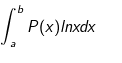
+ Ta đặt u = inx, dv = P(x)dx
– Tính tích phân hàm (e^x) và hàm đa thức P(x) :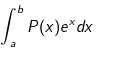
+ Ta đặt u = P(x), dv = e^xdx
– Tính tích phân hàm (e^x) và hàm lượng giác (sinx, cosx) 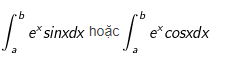
+ Ta đặt u = e^x, dv = sinxdx ( hoặc dv = cosxdx). Tính 2 lần
Bài tập vận dụng :
Bài 1 : Tính tích phân sau :
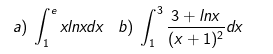
Hướng dẫn giải
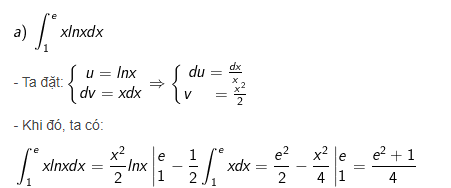
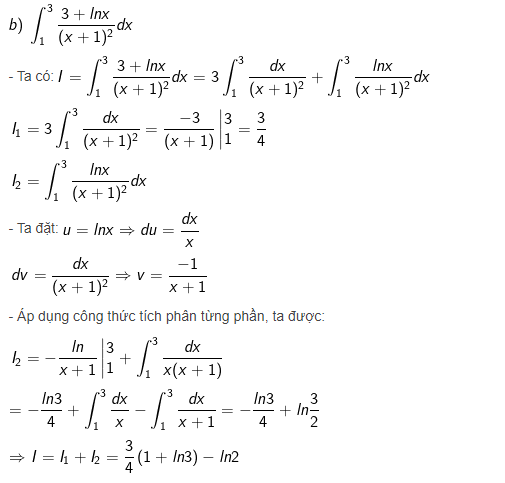
Bài 2 : Tính
![]()
Hướng dẫn giải :
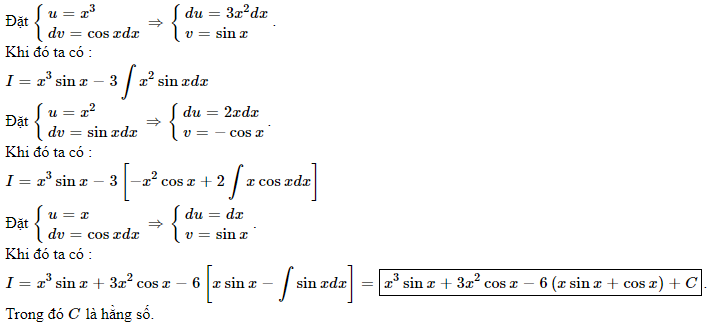
Bài 3 : Tính
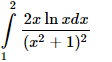
Hướng dẫn giải :
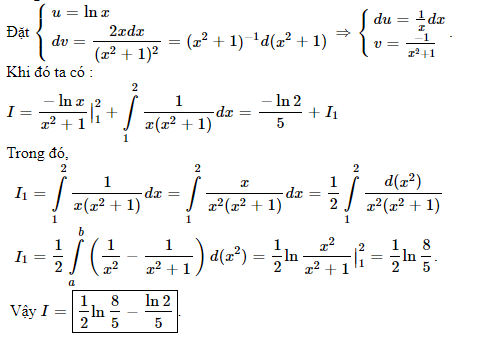
xem thêm tại đây :

