Trong toán học, Định nghĩa của tích phân suy rộng là giới hạn của một tích phân xác định như một điểm đầu nút của (các) khoảng lấy tích phân tiệm cận hoặc số thực xác định hoặc ∞ hoặc -∞ hoặc trong một số trường hợp, cả hai điểm đầu nút đều đạt đến các giới hạn. Một tích phân như vậy thường được viết tượng trưng giống như một tích phân xác định tiêu chuẩn, với vô cực như là một giới hạn của tích phân.Tích phân suy rộng bao gồm 2 loại là tích phân suy rộng với cận vô hạn (tích phân suy rộng loại 1) và tích phân suy rộng của hàm số không bị chặn (tích phân suy rộng loại 2). Sau đây chúng ta cùng nhau đi tìm hiểu kỹ về định nghĩa này nhé.
Một tích phân suy rộng là :
Giả sử f(x) xác định trên [a;+∞) và khả tích trên mọi đoạn hữu hạn a ≤ x ≤ b < +∞
Nếu tồn tại giới hạn (hữu hạn hoặc vô cùng):
![]()
Thì giới hạn này gọi là tích phân suy rộng của f(x) trên [a;+∞).
Nếu giới hạn này là hữu hạn ta nói tích phân suy rộng 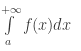
là hội tụ (integral is convergent)
Nếu giới hạn này là vô cùng hoặc không tồn tại ta nói tích phân suy rộng ![]()
là phân kỳ (integral is divergent).
hoặc của dạng :
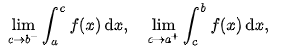
trong đó tích phân nhận một giới hạn của một hay điểm đầu nút khác (hoặc đôi khi cả hai) (Apostol 1967, §10.23). Khi hàm không xác định tại nhiều điểm hữu hạn trong khoảng, tích phân suy rộng trên khoảng được định nghĩa là tổng các tích phân suy rộng trên các khoảng giữa những điểm này.
Ví dụ minh họa
Tính tích phân suy rộng 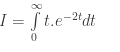
Hướng dẫn giải :
Ta có : 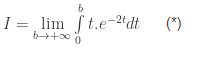
Trước tiên, Tính tích phân 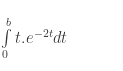
Sử dụng công tức tính phân từng phần ta có: 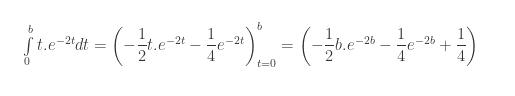
Thế vào (*) ta có: 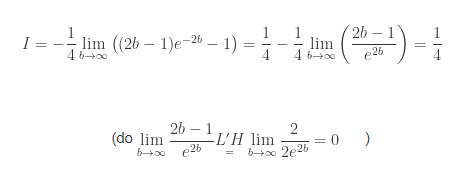
Vậy: I hội tụ và 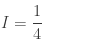
Tích phân quan trọng:
Bài toán xét sự hội tụ của tích phân 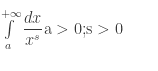
Nếu S > 1 thì tích phân hội tụ
Nếu S < 1 thì tích phân phân kỳ
Xem thêm :
- Tích phân là gì ? , Tính chất và phương pháp tính tích phân
- Cách tìm công thức nguyên hàm của hàm số lượng giác chuẩn
Tiêu chuẩn hội tụ, trường hợp f(x) ≥ 0
Định lý so sánh 1:
Giả sử f(x) và g(x) không âm và khả tích trên [a,b], và f(x) ≤ g(x) ở lân cận +∞ ( tức là x đủ lớn). Khi đó:
– Nếu ![]()
hội tụ thì tích phân hội tụ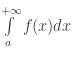
– Nếu ![]()
phân kỳ thì tích phân phân kỳ 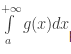
Định lý so sánh 2:
Giả sử f(x) và g(x) không âm và cùng khả tích trên [a,b], và f(x) ≤ g(x) ở lân cận +∞ ( tức là x đủ lớn).
Nếu ![]()
thì hai tích phân cùng hội tụ hoặc cùng phân kỳ.
Nhận xét:
Để xét sự hội tụ của tích phân 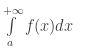
ta cần xây dựng hàm g(x) sao cho ![]()
Nghĩa là, f(x) và g(x) là hai lượng tương đương.
Muốn vậy, ta cần nhận diện và thay thế các VCB, VCL (khi x → +∞ ) có trong f(x) bằng các VCB, VCL tương đương. Tuy nhiên, cần chú ý cả hai hàm f(x) và g(x) phải cùng khả tích trên [a; + ∞).

