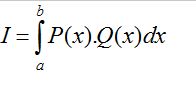Cũng như khái niệm về nguyên hàm, Bài này chúng ta cùng nhau đi tìm hiểu Định nghĩa Tích phân, Tính chất và phương pháp tính tích phân, nó tiếp nối xây dựng trên nền tảng nguyên hàm của một hàm số. Với những kiến thức vô cùng quan trọng trong việc giải quyết các bài tập liên quan đến tích phân cũng như trong các đề thi học kỳ hay các đề thi THPT quốc gia, Mời các bạn cùng đón đọc.
Khái niệm và tính chất
a. Định nghĩa
Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b], hiệu số F(b)−F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a;b] của hàm số f(x).
Kí hiệu là ![]()
Vậy ta có : ![]()
Chú ý : Trong trường hợp a = b, ta định nghĩa:
![]()
Trường hợp a>b, ta định nghĩa : ![]()
Tích phân không phụ thuộc vào chữ dùng làm biến số trong dấu tích phân, tức là :
![]()
b. Tính chất của tích phân
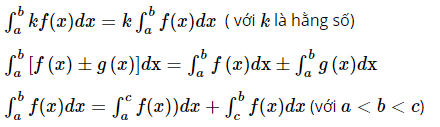
Phương pháp tinh tích phân
Dạng 1: Tính tích phân theo công thức
Ví dụ : Tính các tính phân sau:
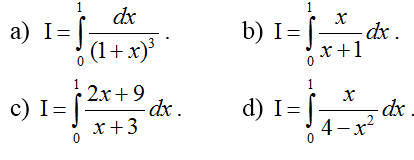
Bài làm :
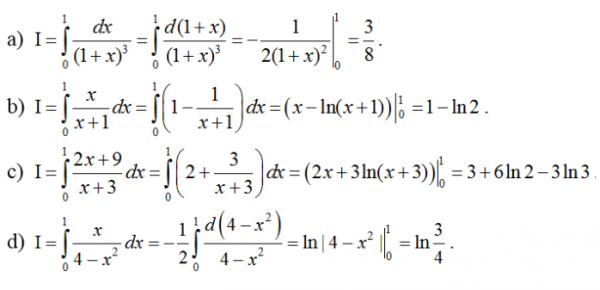

Dạng 2: Phương pháp đổi biến số
1) Đổi biến số dạng 1
Cho hàm số f liên tục trên đoạn [a; b]. Giả sử hàm số u = u(x) có đạo hàm liên tục trên đoạn [a; b] và α ≤ u(x) ≤ β. Giả sử có thể viết f(x) = g(u(x))u'(x), x ∈ [a; b] với g liên tục trên đoạn [α; β]. Khi đó, ta có
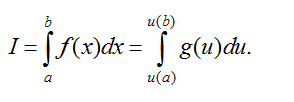
2) Đổi biến số dạng 2
Cho hàm số f liên tục và có đạo hàm trên đoạn [a; b]. Giả sử hàm số x = φ(t) có đạo hàm và liên tục trên đoạn [α; β](*) sao cho φ(α) = a,φ(β) = b và a ≤ φ(t) ≤ b với mọi t ∈ [α; β]. Khi đó:
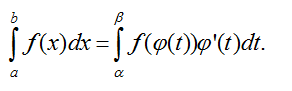
Một số phương pháp đổi biến: Nếu biểu thức dưới dấu tích phân có dạng
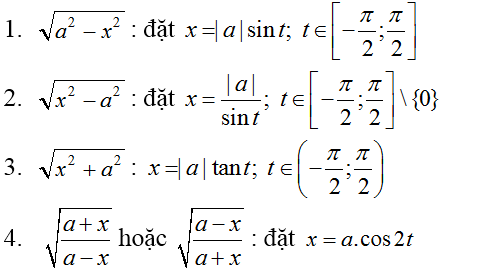
Lưu ý: Chỉ nên sử dụng phép đặt này khi các dấu hiệu 1, 2, 3 đi với x mũ chẵn. Ví dụ, để tính tích phân
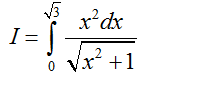
thì phải đổi biến dạng 2 còn với tích phân
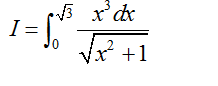
thì nên đổi biến dạng 1.
Chú ý :
- Cách tìm công thức nguyên hàm của hàm số lượng giác chuẩn
- Nguyên hàm là gì? Tính chất và phương pháp tính nguyên hàm
Dạng 3: Dùng tính chất cận trung gian để tính tích phân
Sử dụng tính chất
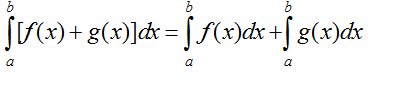
để bỏ dấu giá trị tuyệt đối.
Dạng 4: Phương pháp tính tích phân từng phần.
Định lí : Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm và liên tục trên đoạn [a; b] thì
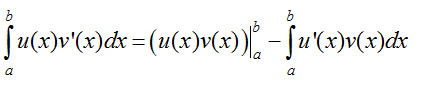
hay viết gọn là
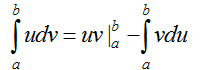
Các dạng cơ bản: Giả sử cần tính