Hàm lượng giác là gì ?
Hai tam giác được coi là đồng dạng nếu một trong hai tam giác có thể thu được nhờ việc mở rộng hay thu hẹp cùng lúc tất cả các cạnh tam giác kia theo cùng tỷ lệ. Điều này chỉ có thể xảy ra khi và chỉ khi các góc tương ứng của chúng bằng nhau. Yếu tố quyết định về sự đồng dạng của tam giác là độ dài các cạnh của chúng tỷ lệ thuận hoặc các góc tương ứng của chúng phải bằng nhau. Điều đó có nghĩa là khi hai tam giác là đồng dạng và cạnh dài nhất của một tam giác lớn gấp 2 lần cạnh dài nhất của tam giác kia thì cạnh ngắn nhất của tam giác thứ nhất cũng lớn gấp 2 lần so với cạnh ngắn nhất của tam giác thứ hai và tương tự như vậy cho cặp cạnh còn lại. Ngoài ra, các tỷ lệ độ dài các cặp cạnh của một tam giác sẽ bằng các tỷ lệ độ dài của các cặp cạnh tương ứng của tam giác còn lại. Cạnh dài nhất của bất kỳ tam giác nào sẽ là cạnh đối của góc lớn nhất.
Hàm lượng giác trong tam giác vuông
Do tổng các góc trong một tam giác là 180 ° hay π radian, nên góc lớn nhất của tam giác vuông là góc vuông. Cạnh dài nhất của tam giác như thế sẽ là cạnh đối của góc vuông và người ta gọi nó là cạnh huyền.
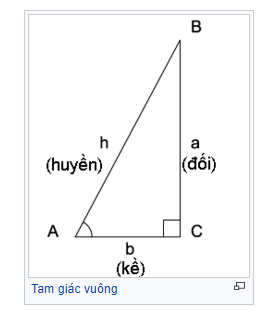
Lấy 2 tam giác vuông có chung nhau một góc thứ hai A. Các tam giác này là đồng dạng, vì thế tỷ lệ của cạnh đối, a, của góc A so với cạnh huyền, h, là như nhau cho cả hai tam giác. Nó sẽ là một số nằm trong khoảng từ 0 tới 1 và nó chỉ phụ thuộc vào chính góc A; người ta gọi nó là sin của góc A và viết nó là sin (A) hay sin A. Tương tự, người ta cũng định nghĩa cosin của góc A như là tỷ lệ của cạnh kề, b, của góc A so với cạnh huyền, h, và viết nó là cos (A) hay cos A.
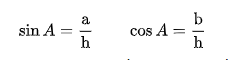
Đây là những hàm số quan trọng nhất trong lượng giác; các hàm số khác có thể được định nghĩa theo cách lấy tỷ lệ của các cạnh còn lại của tam giác vuông nhưng chúng có thể biểu diễn được theo sin và cosin.
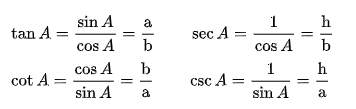
Các hàm lượng giác như trên đã nói đã được định nghĩa cho các góc nằm trong khoảng từ 0 tới 90 ° (0 tới π/2 radian). Sử dụng khái niệm vectơ cho đường tròn đơn vị, người ta có thể mở rộng chúng để có các đối số âm và dương
Nguồn : https://vi.wikipedia.org/
Hệ thức lượng giác trong tam giác .
Hệ thức lượng giác trong tam giác vuông .
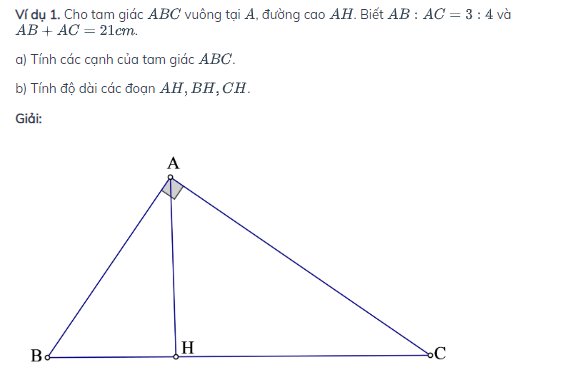
Hệ thức lượng trong tam giác vuông sẽ giúp các bạn giải quyết các bài toán liên quan đến hệ thức lượng trong tam giác vuông.
Trong tam giác vuông ABC như hình dưới gọi c,b là độ dài hình chiếu các cạnh góc vuông lên cạnh huyền ta có hệ thức như sau :
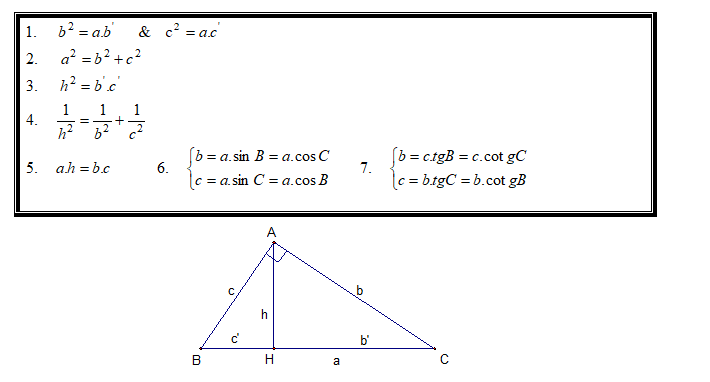
Hệ thức lượng giác trong tam giác thường .
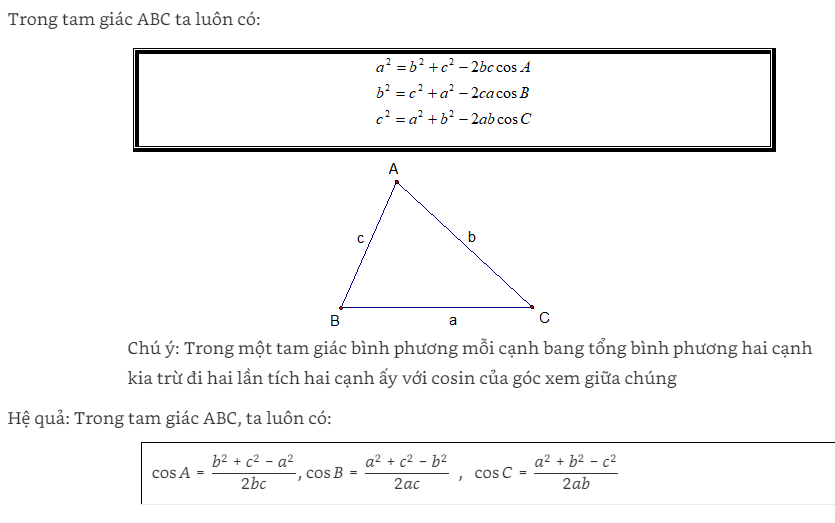
Định lý hàm Cosin
Định lý hàm Sin

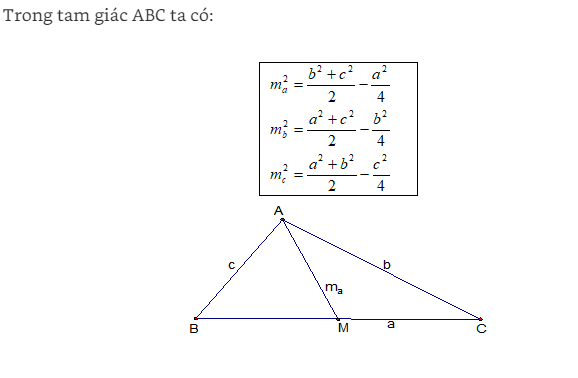
Định Lý về đường trung tuyến
Định lý về diện tích tam giác

Định lý về đường phân giác
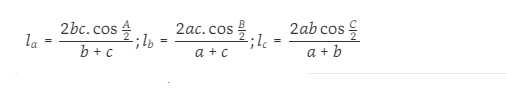
Ví dụ