Bài học ngày hôm nay chúng ta sẽ cùng tìm hiểu về diện tích hình nón trong đó có diện tích toàn phần hình nón và diện tích xung quanh hình nón . Bài học này các em đặc biệt cần chú ý đến công thức tính diện tích xung quanh hình nón và công thức tính diện tích toàn phần hình nón để áp dụng vào các bài tập nhé .
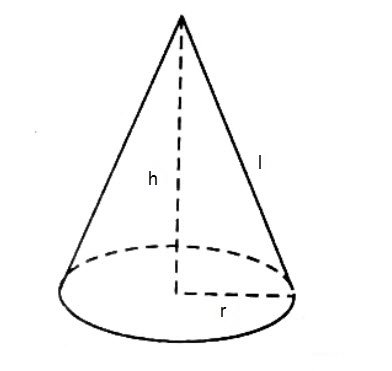
Diện tích hình nón là gì ?
Hình nón được tạo ra khi quay một tam giác vuông một vòng quanh cạnh góc vuông cố định. Khi này diện tích hình nón được biết đến với diện tích xung quanh và diện tích toàn phần hình nón được phát biểu như sau :
Diện tích xung quanh hình nón chỉ bao gồm diện tích mặt xung quanh, bao quanh hình nón, không gồm diện tích đáy.
Diện tích toàn phần được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích đáy tròn.
Công thức tính diện tích xung quanh hình nón .
Công thức tính diện tích xung quanh hình nón được tính như sau :
S ( xung quanh ) = π.r.l
Trong đó :
S ( xung quanh ) : là diện tích xung quanh hình nón
π: là hằng số Pi = 3,14
r: Bán kính vòng tròn đáy hình nón
l: đường sinh của hình nón
Phát biểu bằng lời : Diện tích xung quanh hình nón bằng tích của Pi nhân với bán kính đáy hình nón nhân với đường sinh hình nón .
Ví dụ tính diện tích xung quanh hình nón
Cho hình nón có độ dài đường sinh là 10cm, bán kính vòng tròn đáy hình nón là 6cm. Tính diện tích xung quanh hình nón .
Lời giải : theo đề bài ta có : l = 10cm , r = 6cm
áp dụng công thức :S ( xung quanh ) = π.r.l = π x 10 x 6 = 60π ( cm)²
Công thức tính diện tích toàn phần hình nón .
Công thức : S ( toàn phần ) = π.r.l + π.r² hay S ( toàn phần ) = S ( xung quanh ) + S ( đáy )
Trong đó :
S ( toàn phần ) : là diện tích toàn phần hình nón
π: là hằng số Pi = 3,14
r: Bán kính đáy hình nón
l: độ dài đường sinh hình nón
Ví dụ tính diện tích toàn phần hình nón
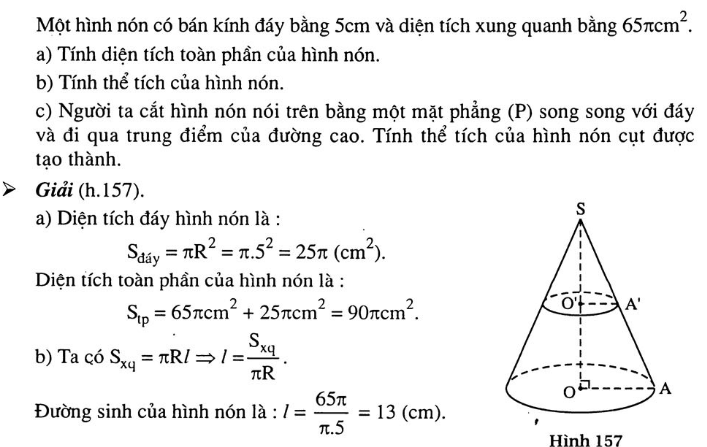
Kết luận : Trên đây là toàn bộ công thức tính diện tích toàn phần hình nón và công thức tính diện tích xung quanh hình nón kèm ví dụ thực tế , các em cần chú ý áp dụng công thức để gải các bài tập về diện tích hình nón .
