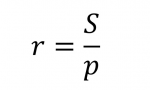Công thức tính bán kính đường tròn nội tiếp tam giác tuy rất đơn giản nhưng luôn có trong các đề thi của các em vì vậy muốn tính được đường tròn nội tiếp tam giác các bạn cần ghi nhớ công thức và cách tính đường tròn nội tiếp tam giác sao cho nhanh nhất để làm bài tập của mình. Hãy cùng chúng tôi tìm hiểu kiến thức này nhé!
Đường tròn nội tiếp tam giác là gì?
Trong hình học, đường tròn nội tiếp của một tam giác là đường tròn lớn nhất nằm trong tam giác, nó tiếp xúc với cả ba cạnh của tam giác. Tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác trong.
Tính chất đường tròn nội tiếp tam giác
- Tâm đường tròn nội tiếp tam giác chính là giao điểm của ba đường phân giác.
- Trong tam giác đều thì tâm của đường tròn nội tiếp và đường tròn ngoại tiếp trùng nhau.
Công thức tính bán kính đường tròn nội tiếp tam giác
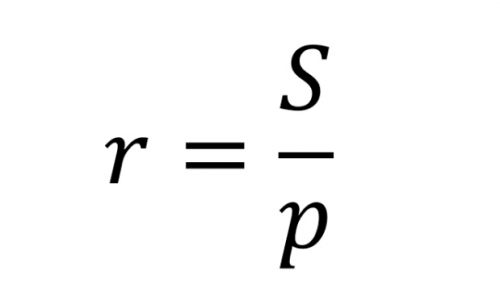
Trong đó:
- S: Diện tích tam giác.
- p: Nửa chu vi tam giác.
Phát biểu bằng lời : Công thức tính bán kính đường tròn nội tiếp tam giác là diện tích tam giác chia cho nửa chu vi.
Bài tập ví dụ cách tính đường tròn nội tiếp tam giác
Ví dụ 1: Cho hình tam giác △ABC có độ dài các cạnh của hình tam giác lần lượt là là 8cm, 10cm, 12cm. Xác định bán kính đường tròn nội tiếp tam giác △ABC bằng bao nhiêu?
Lời giải:
Áp dụng công thức chu vi tam giác ta có, chu vi △ABC là:
P= 8 + 10 + 12 = 30 (cm)
⇒ nửa chu vi của △ABC là: p = 30 : 2= 15 (cm)
Áp dụng công thức ta có bán kính đường tròn nội tiếp △ABC là:
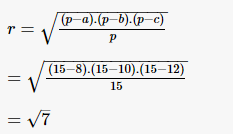
Ví dụ 2 : Cho tam giác MNP biết MN = 8cm, MP = 9cm, NP = 11cm. Hỏi bán kính đường tròn nội tiếp tam giác MNP bằng bao nhiêu?
Lời giải

Ví dụ 3 : Cho tam giác MNP đều cạnh 2a, Hỏi bán kính đường tròn nội tiếp tam giác MNP bằng bao nhiêu?
Lời giải
Diện tích tam giác đều MNP là:
S = ½ MN.MP.sinM
= ½ .2a.2a.sin60º
= a2√3
Nửa chu vi tam giác MNP là:

Như vậy trên đây chúng tôi đã giới thiệu đầy đủ về tính chất và công thức tính đường tròn nội tiếp tam giác kèm bài tập ví dụ đầy đủ nhất cho các em tham khảo nhé!