Nội dung bài viết Tìm 2 số khi biết tổng và tích bao gồm công thức phương pháp giải bài tập một cách đầy đủ và chính xác nhất. Hi vọng những kiến thức này sẽ giúp các bạn giải quyết được bài tập một cách nhanh chóng nhất.
Tìm hiểu thêm:
Cách tìm hai số khi biết tổng và tích
Phương pháp giải
Để tìm hai số khi biết tổng và tích của chúng, bạn có thể sử dụng phương trình bậc hai. Hãy xem cách làm như sau:
Giả sử hai số cần tìm là x và y. Ta biết tổng của hai số đó là S và tích của chúng là P. Ta có các phương trình sau đây:
x + y = S
x * y = P

Giải hệ phương trình này để tìm x và y.
Ví dụ:
Cho tổng S = 7 và tích P = 12.
Ta có hệ phương trình:
x + y = 7
x * y = 12
Giải phương trình thứ nhất để tìm x hoặc y:
x = 7 – y
Thay x vào phương trình thứ hai:
(7 – y) * y = 12
Mở ngoặc và đưa phương trình về dạng bậc hai:
y^2 – 7y + 12 = 0
Giải phương trình bậc hai này để tìm giá trị của y. Sau đó, thay giá trị y vào phương trình x = 7 – y để tìm giá trị của x.
Bài tập tự luận
Câu 1 :
Tìm hai số u và v biết
a. u + v = 15 và u.v = 36
b. u + v = 4 và u.v = 7
c. u + v = -12 và u.v = 20
Hướng dẫn giải
a. Với S = 15, P = 36 thì S2 = 225 > 4P = 144 nên tồn tại hai số u và v
Hai số u và v là nghiệm của phương trình: x2 – 15x + 36 = 0
∆ = (-15)2 – 4.36 = 225 – 144 = 81 > 0
Suy ra phương trình có 2 nghiệm phân biệt:
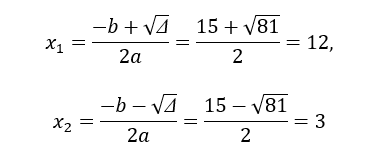
Vậy hai số cần tìm là: u = 12, v = 3 hoặc u = 3, v = 12
b. Với S = 4, P = 7 thì S2 = 16 < 4P = 28 nên không tồn tại hai số u,v thỏa
mãn yêu cầu của đề bài
c. Với S = -12, P = 20 thì S2 = 144 > 4P = 80 nên tồn tại hai số u và v
Hai số u và v là nghiệm của phương trình x2 + 12x + 20 = 0
∆ = (12)2 – 4.20 = 144 – 80 = 64 > 0
Suy ra phương trình có 2 nghiệm phân biệt
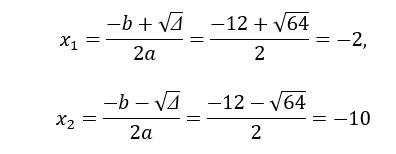
Vậy hai số cần tìm là: u = -2, v = -10 hoặc u = -10, v = -2
Câu 2 : Tìm hai số x, y biết x2 + y2 = 61 và xy = 30
Hướng dẫn giải
Theo giả thiết ta có:
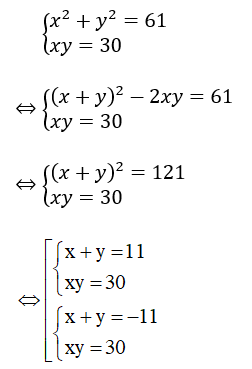
+ Xét TH1: x + y = 11 và xy = 30
Với S = 11, P = 30 thì S2 = 121 > 4P = 120 nên tồn tại hai số x và y
Hai số x và y là nghiệm của phương trình x2 – 11x + 30 = 0
∆ = (11)2 – 4.30 = 121 – 120 = 1 > 0
Suy ra phương trình có 2 nghiệm phân biệt
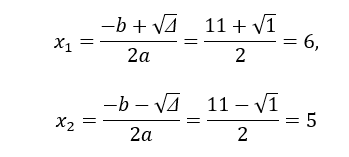
Vậy hai số cần tìm là: x = 5, y = 6 hoặc x = 6, y = 5
+ Xét TH2: x + y = -11 và xy = 30
Với S = -11, P = 30 thì S2 = 121 > 4P = 120 nên tồn tại hai số x và y
Hai số x và y là nghiệm của phương trình: x2 + 11x + 30 = 0
∆ = (-11)2 – 4.30 = 121 – 120 = 1 > 0
Suy ra phương trình có 2 nghiệm phân biệt:
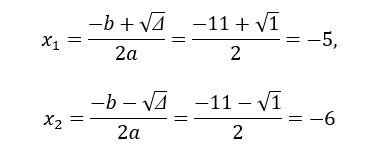
Vậy hai số cần tìm là: x = -5, y = -6 hoặc x = -6, y = -5
Kết hợp 2 trường hợp ta tìm được 4 cặp số x,y thỏa mãn đầu bài
x = 5, y = 6 hoặc x = 6, y = 5 hoặc x = -5, y = -6 hoặc x = -6, y = -5

