Giải bất phương trình chứa dấu giá trị tuyệt đối trong toán lớp 8 là dạng bài tập mà học sinh gặp phải nhiều. Trọng dạng bài tập này các em phải bỏ dấu giá trị tuyệt đối và rút gọn biểu thức… Xem ngay bài phương trình chứa dấu giá trị tuyệt đối để có phương pháp giải bài tập chính xác.

Phương trình chứa dấu giá trị tuyệt đối
Giá trị tuyệt đối
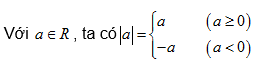
Dấu của nhị thức bậc nhất
Định nghĩa : Nhị thức bậc nhất của x là biểu thức có dạng:
![]()
Trong đó : a, b là các số cho trước và a ≠ 0
![]()
Gọi là nghiệm của nhị thức bậc nhất f(x).
Quy tắc dấu
Nhị thức bậc nhất f(x) = ax + b cùng dấu với a khi x > x (o) và trái dấu với a khi x < x (o):
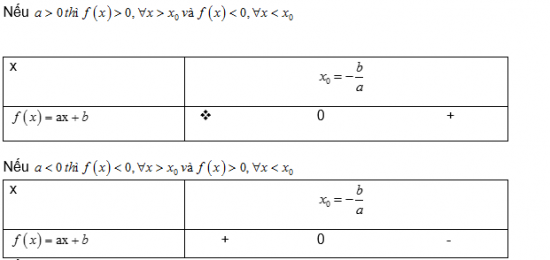
Bài tập ví dụ
Ví dụ 1 : Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức sau:
a) A = | x – 1 | + 3 – x khi x ≥ 1.
b) B = 3x – 1 + | – 2x | khi x < 0.
Lời giải
a) Khi x ≥ 1 ta có x – 1 ≥ 0 nên | x – 1 | = x – 1
Do đó A = | x – 1 | + 3 – x = x – 1 + 3 – x = 2.
b) Khi x < 0 ta có – 2x > 0 nên | – 2x | = – 2x
Do đó B = 3x – 1 + | – 2x | = 3x – 1 – 2x = x – 1.
Ví dụ 2 : Giải các phương trình sau:
a) |2x| = x – 6 ; b) |−3x| = x – 8
b) |−3x| = x – 8 ;
c) |4x| = 2x + 12 ; d) |−5x| – 16 = 3x.
d) |−5x| – 16 = 3x.
Lời giải
a) |2x| = x – 6
Ta có: 2x = x – 6 ⇔ x = – 6 khi x ≥ 0
Giá trị x = – 6 không thỏa mãn điều kiện x ≥ 0 nên x = – 6 không phải là nghiệm của phương trình
– 2x = x – 6 ⇔ x = 2 khi x < 0
Giá trị x = 2 không thỏa mãn điều kiện x < 0 nên x = 2 không phải là nghiệm của phương trình
Vậy tập nghiệm của phương trình là S = ⊘
b) |−3x| = x – 8
Ta có: 3x = x – 8 ⇔ x = – 4 khi x ≥ 0
Giá trị x = -4 không thỏa mãn điều kiện x ≥ 0 nên x = – 4 không phải là nghiệm của phương trình
– 3x = x – 8 ⇔ x = 2 khi x < 0
Giá trị x = 2 không thỏa mãn điều kiện x < 0 nên x = 2 không phải là nghiệm của phương trình
Vậy tập nghiệm của phương trình là S = ⊘
c) |4x| = 2x + 12
Ta có: 4x = 2x + 12 ⇔ x = 6 khi x ≥ 0
Giá trị x = 6 thỏa mãn điều kiện x ≥ 0 nên x = 6 là nghiệm của phương trình
– 4x = 2x + 12 ⇔ x = – 2 khi x < 0
Giá trị x = – 2 thỏa mãn điều kiện x < 0 nên x = – 2 là nghiệm của phương trình
Vậy tập nghiệm của phương trình là S = {- 2; 6}.
d) |−5x| – 16 = 3x
Ta có: 5x – 16 = 3x ⇔ x = – 2 khi x ≥ 0
Giá trị x = 8 thỏa mãn điều kiện x ≥ 0 nên x = 8 là nghiệm của phương trình
– 5x – 16 = 3x ⇔ x = – 2 khi x < 0
Giá trị x = – 2 thỏa mãn điều kiện x < 0 nên x = – 2 là nghiệm của phương trình
Vậy tập nghiệm của phương trình là S = {- 2; 8}

