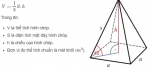
Thể tích khối chóp được tính theo công thức nào? Bài viết này chúng tôi sẽ hướng dẫn cho anh chị công thức và bài tập cách tính thể tích hình chóp để học sinh có thể ghi nhớ và áp dụng giải bài tập ngay.
Thể tích hình chóp

Nhận biết hình chóp
Hình chóp là : Một đa giác (tam giác, tứ giác, lục giác, … ) có các điểm nối với một điểm khác ngoài đa giác được gọi là hình chóp (hay khối chóp). Đa giác được gọi là mặt đáy và điểm nằm ngoài đa giác được gọi là đỉnh của hình chóp.
Tính chất hình chóp
Hình chóp tam giác là hình chóp có đáy là tam giác.
hình chóp tứ giác là hình chóp có đáy là tứ giác.
hình chóp tam giác đều là hình chóp đáy là tam giác đều.
hình chóp tứ giác đều là hình chóp có đấy là tứ giác đều.
…..
Hình chóp cụt là hình được tạo bởi thiết diện của một mặt phẳng song song với đáy của hình chóp.
Công thức tính thể tích hình chóp
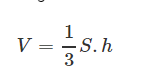
Trong đó:
V : là thể tích hình chóp
S : là diện tích mặt đáy hình chóp
h : là chiều co hình chóp
Công thức tính thể tích hình chóp cụt:
Tính thể tích hình chóp cụt ta áp dụng công thức sau :
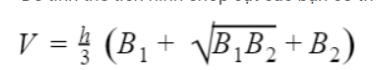
- V : là thể tích hình chóp cụt
- h : Là chiều cao hình chóp cụt
- B1, B2 : là diện tích của đáy hình chóp cụt
Đơn vị đo, kí hiệu thể tích hình chóp
+ Đơn vị đo thể tích hình chóp được tính bằng : m³
+ Kí hiệu tính thể tích hình chóp : V
Bài tập về cách tính thể tích hình chóp
Tính thể tích khối chóp có mặt bên vuông góc với đáy
Bài toán này còn có thể được cho dưới dạng cho hai mặt bên cùng vuông góc với đáy. Khi đó chiều cao của khối chóp chính là giao tuyến của hai mặt đó.
Đối với khối chóp có mặt bên (SAB) vuông góc với đáy thì đường cao của hình chóp là SH. Trong đó H thuộc đường thẳng AB. Và vấn đề của chúng ta thường là phải xác định vị trí điểm H. Thông thường điểm H là 1 điểm đặc biệt nằm trên đường AB. Còn trong trường hợp chúng ta không xác định được điểm H thì chúng ta có thể vận dụng các hệ thức lượng trong tam giác để tính độ dài SH.
Tính thể tích khối chóp đều
Khối chóp đều là khối chóp có đáy là đa giác đều và hình chiếu của đỉnh lên mặt đáy trùng với tâm của đáy. Nếu đáy là tam giác đều thì tâm thường xác định là trọng tâm tam giác. Tứ giác đều chính là hình vuông và tâm là giao hai đường chéo. Thường người ta cũng chỉ xoay quanh hai kiểu đáy tam giác và tứ giác thôi.
Bài tập ví dụ tính thể tích khối chóp
Ví dụ 1 : Cho hình chó S. ABC có đáy ABC là tam giác đều cạnh a. các cạnh bên bằng nhau và bằng 2a. tính thể tích hình chóp này?
Bài giải
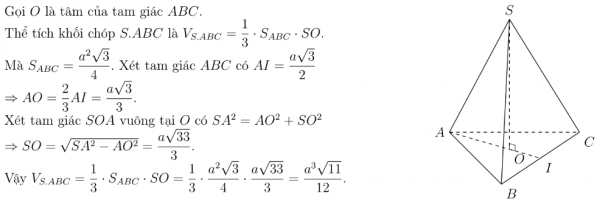
Ví dụ 2 : Cho hình chóp S.ABC có SA vuông góc mặt đáy, tam giácABC vuông tại A, SA = 2 cm, AB = 4cm, AC = 3 cm. Tính thể tích khối chóp.
Lời giải:
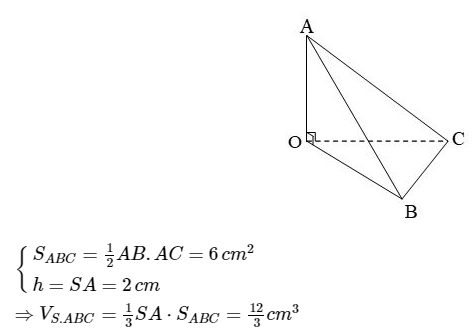
Trên đây là toàn bộ công thức tính thể tích hình chóp và thể tích hình chóp cụt kèm bài tập ví dụ để các em dễ hiểu hơn. Hi vọng những chia sẻ này sẽ giúp ích được các bạn áp dụng vào bài tập.