Hàm số bậc nhất là gì?
Định nghĩa : Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a,b là những số cho trước, a ≠ 0
Đặc biệt, khi b = 0 thì hàm số bậc nhất trở thành hàm số y = ax, biểu thị tương quan tỉ lệ thuận giữa y và x.
Tính chất : Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có tính chất sau:
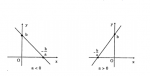
Đồng biến trên R khi a > 0
Nghịch biến trên R khi a < 0.
Vẽ đồ thị hàm số y = ax + b
Trường hợp 1: Khi b=0
Khi b = 0 thì y =ã là đường thẳng di qua gốc tọa độ O(0;0) và điểm A (1;a) đã biết
Xét trường hợp y= ax với a khác 0 và b khác 0
Ta đã biết đồ thị hàm số y = ax + b là một đường thẳng, do đó về nguyên tắc ta chỉ cần xác định được hai điểm phân biệt nào đó của đồ thị rồi vẽ đường thẳng qua hai điểm đó
Cách thứ nhất:
Xác định hai điểm bất kỳ của đồ thị , chẳng hạn:
Cho x = 1 tính được y = a + b, ta có điểm A ( 1; a+b)
Cho x = -1 tính được y = -a + b, ta có điểm B (-1 ; -a + b)
Cách thứ hai:
Xác định giao điểm của đồ thị với hai trục tọa dộ:
Cho x = 0 tính được y = b, ta được điểm C (-b/a;0)
Cho y = 0 tính được x = -b/ a, ta có điểm D (-b/a; 0)
Vẽ đường thẳng qua A, B hoặc C, D ta được đồ thị của hàm số y = ax + b
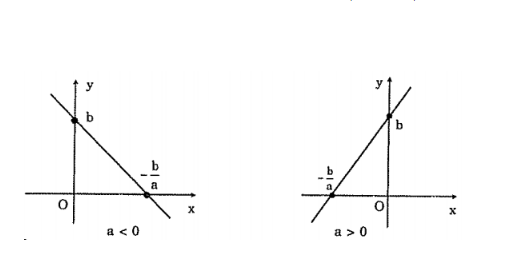
Dạng đồ thị của hàm số y = ax + b ( a khác 0)
Trường hợp 2: Khi b khác 0
Ta cần xác định hai điểm phân biệt bất kì thuộc đồ thị.
Bước 1: Cho x=0=>y=b. Ta được điểm P(0;b)∈Oy.
Cho y=0=>x=−ba. Ta được Q(−ba;0)∈0x.
Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q, ta được đồ thị của hàm số y=ax+b.
Các dạng bài tập hàm số bậc nhất

Bài tập ví dụ:
Ví dụ 1 : Cho hàm số y = ( m-1 ) . Tìm m để hàm số đồng biến, nghịch biến trên R
Bài giải:
Hàm số đồng biến trên: R ⇔ m-1 > 0 m>1
Hàm số nghịch biến trên : R ⇔ m-1< m < 1