Bài toán tính tích phận chắc chắn sẽ có trong các kỳ thi trung học phổ thông và kỳ thi đại học, nó có thể ở dạng cơ bản hoặc nâng cao. Để nắm kỹ kiến thức này các em cần nhớ bảng tích phân và cách tính tích phân để rồi áp dụng vào các bài giải toán. Dưới đây là đầy đủ công thức tích phân từ cơ bản đến mở rộng cho các em tham khảo nhé!
Bảng công thức tích phân đầy đủ
Bạn có thể quan tâm
Khái niệm tích phân
Cho hàm f(x) liên tục trên một khoảng xác định, được kí hiệu là K và a, b là hai số thực bất kì thuộc khoảng K đó. Nếu F(x) là một nguyên hàm của f(x) thì hiệu số F(b)−F(a) được gọi là tích phân của f(x) trong khoảng từ a đến b và được ký hiệu như sau:
Từ đó, ta có ký hiệu như sau: ∫f(x)dx.
Tính chất của tích phân
Giả sử cho hai hàm số f(x) và g(x) liên tục trên K và a, b, c là ba số bất kỳ thuộc K. Khi đó ta có :
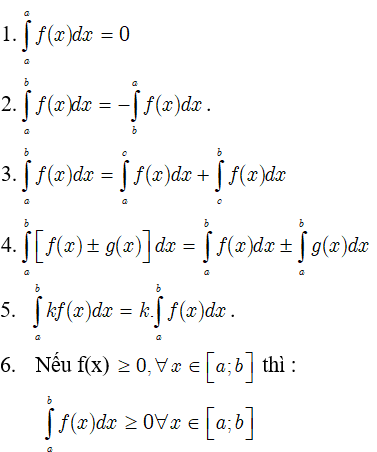
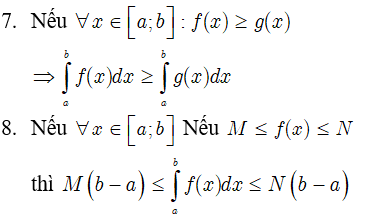
Công thức tính phân cơ bản

Bảng tích phân từng phần

Bảng tích phân lượng giác

Tích phân xác định

Tích phân mở rộng
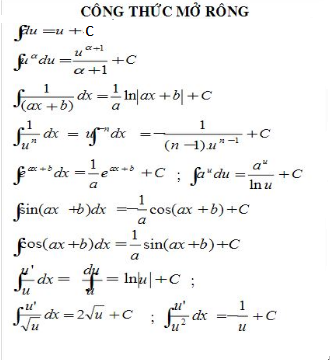
Tích phân không xác định

Tích phân hàm số hữu tỉ

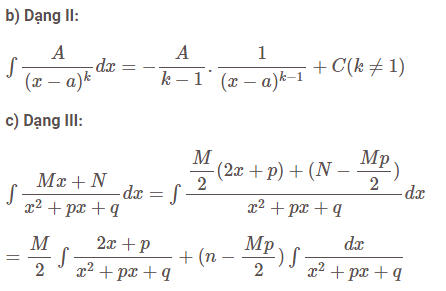
Trên đây là 6 công thức tích phân từ cơ bản đến nâng cao mở rộng để các bạn cùng tham khảo nhé.
Cách tính tích phân
Cách 1 : Dùng phương pháp phân tích

Cách 2 : Phương pháp biến đổi số

Cách 3 : Phương pháp vi phân

Cách 4 : Phương pháp tính của tích phân từng phần

Trên đây là 4 cách tính tích phân mà chúng ta có thể áp dụng vào bài tập nhuần nhuyễn nhất các e có thể tìm các bài tập trên internet hoặc các bài tập trong sách giáo khoa để áp dụng vào từng cách tính sao cho ra kết quả nhanh và chính xác nhất khi vào bài thi làm các đáp án trắc nghiệm sẽ rút ngắn được thời gian.

