Có thể nói bảng nguyên hàm cực kỳ quan trọng trong các kỳ thi của các em vì vậy công thức nguyên hàm cơ bản, nâng cao chúng ta cần phải lắm kỹ được những kiến thức này mới có được kết quả tốt trong trương trình trung học phổ thông nhé!
Bảng Nguyên Hàm

Định nghĩa nguyên hàm
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
- Kí hiệu: ∫ f(x)dx = F(x) + C.
Tính chất nguyên hàm
- (∫ f(x)dx)’ = f(x) và ∫ f'(x)dx = f(x) + C.
- Nếu F(x) có đạo hàm thì: ∫d(F(x)) = F(x) + C).
- ∫ kf(x)dx = k∫ f(x)dx với k là hằng số khác 0.
- ∫[f(x) ± g(x)]dx = ∫ f(x)dx ± ∫g(x)dx.
Định Lý nguyên hàm
- Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
- Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
⇒ F(x) + C; C ∈ R là họ tất cả các nguyên hàm của f(x) trên K.
Bảng nguyên hàm từ cơ bản đến nâng cao
Bảng nguyên hàm cơ bản
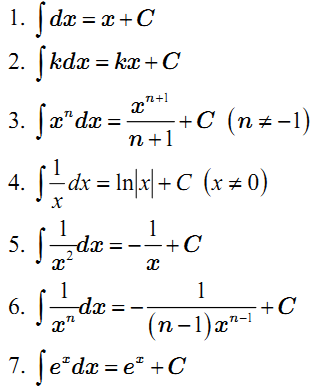
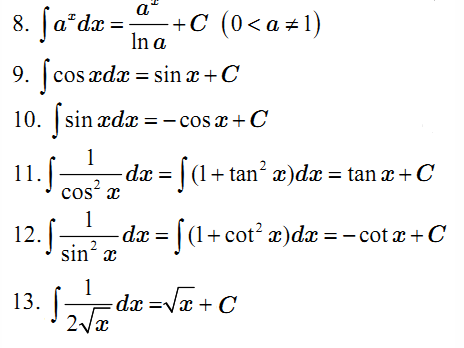
Bảng Nguyên Hàm Nâng Cao a ≠ 0

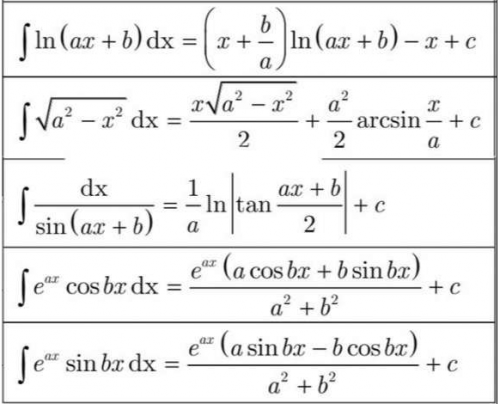
Bảng nguyên hàm mở rộng
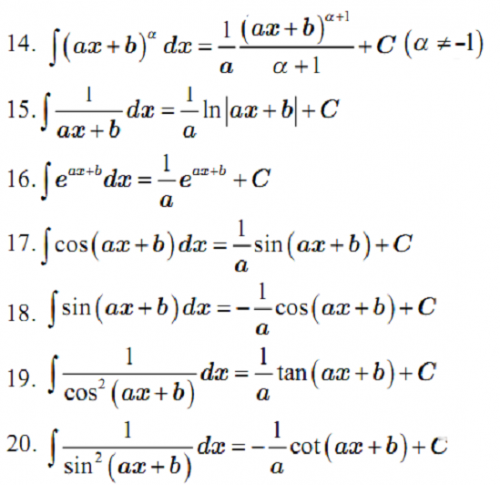
Các bảng nguyên hàm mở rộng khác
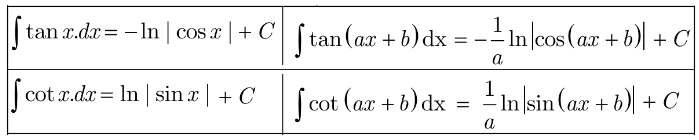
chúng ta áp dụng tính chất sau : Nếu F(x) là nguyên hàm của f(x) thì:
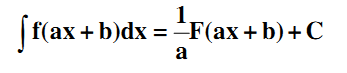
Việc phải học thuộc và giải bài toán thành thạo với bảng nguyên hàm là điều bắt buộc đối với các em. Các em hãy liệt kê các công thức thường dùng để có thể dễ dàng xem lại khi cần và xem các dạng toán dưới đây.
5 dạng bài tập về bảng nguyên hàm
Tính nguyên hàm bằng bảng nguyên hàm
- Tính nguyên hàm bằng bảng nguyên hàm
- Tìm nguyên hàm F(x) của hàm số f(x): Nhóm công thức cơ bản.
- Tìm nguyên hàm F(x) của hàm số f(x): Nhóm công thức có mẫu số cơ bản.
- Tìm nguyên hàm F(x) của hàm số f(x): Nhóm công thức nguyên hàm của hàm lượng giác.
- Tìm nguyên hàm F(x) của hàm số f(x): Nhóm công thức mũ.
Nguyên hàm của số hữu tỷ
- Tìm nguyên hàm F(x) của hàm số f(x): Nhóm hàm hữu tỉ không chứa căn thức.
Nguyên hàm từng phần
- Tìm nguyên hàm F(x) của hàm số f(x) bằng phương pháp nguyên hàm từng phần.
Nguyên hàm đổi biến số
- Tìm nguyên hàm F(x) của hàm số f(x): Nhóm hàm số mũ.
- Tìm nguyên hàm F(x) của hàm số f(x): Nhóm hàm số chứa căn thức.
- Tìm nguyên hàm F(x) của hàm số f(x): Nhóm hàm số chứa logarit.
- Tìm nguyên hàm F(x) của hàm số f(x): Nhóm hàm số chứa e^x.
- Tìm nguyên hàm F(x) của hàm số f(x): Đổi biến hàm số lượng giác.
Tính chất nguyên hàm và nguyên hàm của hàm ẩn
- Sử dụng định nghĩa F'(x) = f(x).
- Sử dụng định nghĩa giải bài toán nguyên hàm của hàm ẩn.
Trên đây là 5 dạng toán nguyên hàm để các e có thể tìm hiểu và áp dụng vào các bài tập đặc biệt và việc phải học thuộc bảng nguyên hàm từ cơ bản đến nâng cao là điều rất quan trọng.

