Hàm số lượng giác sin và hàm số lượng giác côsin
1 . Hàm số lượng giác sin
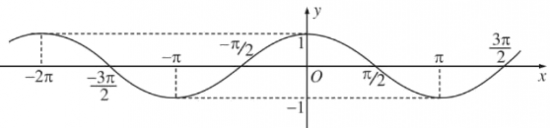
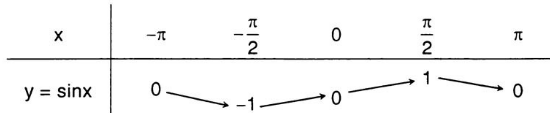
Hàm số y=sinx có tập xác định R là −1≤sinx≤1,∀x∈R.
y=sinx là hàm số lẻ.
y=sinx là hàm số tuần hoàn với chu kì 2π.
Hàm số y=sinx nhận các giá trị đặc biệt:
* sinx=0 khi x=kπ,k∈Z.
* sinx=1 khi x=π2+k2π,k∈Z.
* sinx=−1 khi x=−π2+k2π,k∈Z.
Công thức hàm số y= sinx
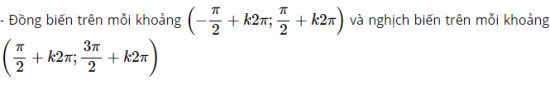
Đồ thị hàm số y=sinx:
- Là hàm số lẻ
- Là hàm số tuần hoàn với chu kì 2π
Bảng biến thiên của hàm số y = sinx trên đoạn [ -π; π ]
2. Hàm số lượng giác côsin
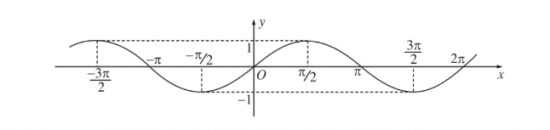
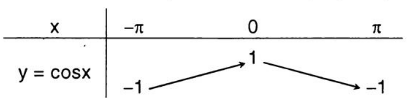
Hàm số y=cosx có tập xác định R là −1≤cosx≤1,∀x∈R.
y=cosx là hàm số chẵn.
y=cosx là hàm số tuần hoàn với chu kì 2π.
Hàm số y=cosx nhận các giá trị đặc biệt:
+ cosx=0 khi x=π2+kπ,k∈Z .
+ cosx=1 khi x=k2π,k∈Z.
+ cosx=−1 khi x=(2k+1)π,k∈Z.
Công thức hàm số y = Cosx
![]()
Đồ thị hàm số y=cosx:
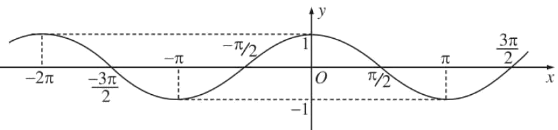
- Là hàm số chẵn
- Là hàm số tuần hoàn với chu kì 2π
Bảng biến thiên của hàm số y = cosx trên đoạn [ -π ; π ]
Hàm số lượng giác tang và côtang
1. Hàm số lượng giác tang
Hàm số y=tanx=sinxcosx có tập xác định R là D=R∖{π2+kπ,k∈Z}.
y=tanx là hàm số lẻ.
y=tanx là hàm số tuần hoàn với chu kì π.
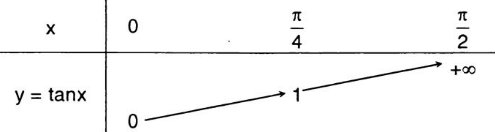
Hàm số y=tanx nhận các giá trị đặc biệt:
+ tanx=0 khi x=kπ,k∈Z.
+ tanx=1 khi x=π4+kπ,k∈Z.
+ tanx=−1 khi x=−π4+kπ,k∈Z .
Công thức hàm số y = tanx
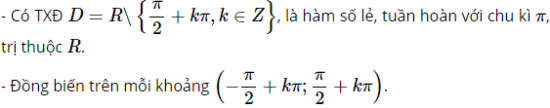
Đồ thị hàm số y=tanx:
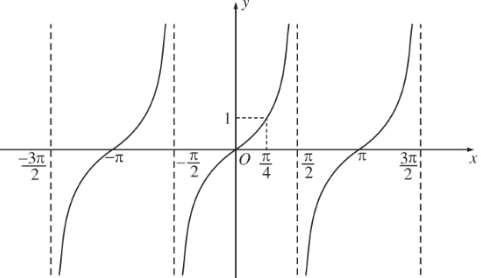
- Là hàm số lẻ
- Là hàm số tuần hoàn với chu kì π
Bảng biến thiên của hàm số y = tanx trên [ 0; π/2)
2. Hàm số lượng giác côtang
Hàm số y=cotx=cosxsinx có tập xác định R là D=R∖{kπ,k∈Z}.
y=cotx là hàm số lẻ.
y=cotx là hàm số tuần hoàn với chu kì π.
Hàm số y=cotx nhận các giá trị đặc biệt:
+ cotx=0 khi x=π2+kπ,k∈Z.
+ cotx=1 khi x=π4+kπ,k∈Z.
+ cotx=−1 khi x=−π4+kπ,k∈Z.
Công thức hàm số y = cotx
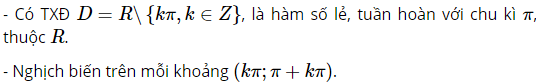
Đồ thị hàm số y=cotx:
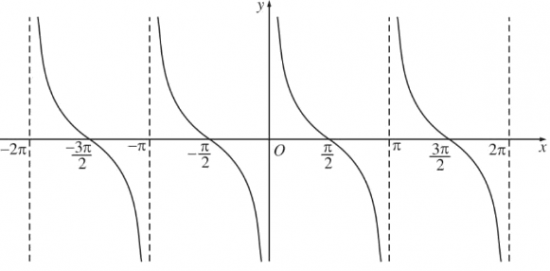
- Là hàm số lẻ
- Là hàm số tuần hoàn với chu kì π
Sự biến thiên và đồ thị của hàm số y = cotx trên khoảng ( 0 đến π)